24 Modelización de epidemias
24.1 Resumen
Existe un conjunto creciente de herramientas para la modelización de epidemias que nos permite realizar análisis bastante complejos con un esfuerzo mínimo. En esta sección se ofrece una visión general de cómo utilizar estas herramientas para:
estimar el número de reproducción efectivo Rt y las estadísticas relacionadas, como el tiempo de duplicación
elaborar proyecciones a corto plazo de la incidencia futura
No pretende ser una visión general de las metodologías y los métodos estadísticos en los que se basan estas herramientas, así que consulta la sección de Recursos para ver los enlaces a algunos documentos que cubren esto. Asegúrese de que conoce los métodos antes de utilizar estas herramientas, ya que así podrá interpretar con precisión sus resultados.
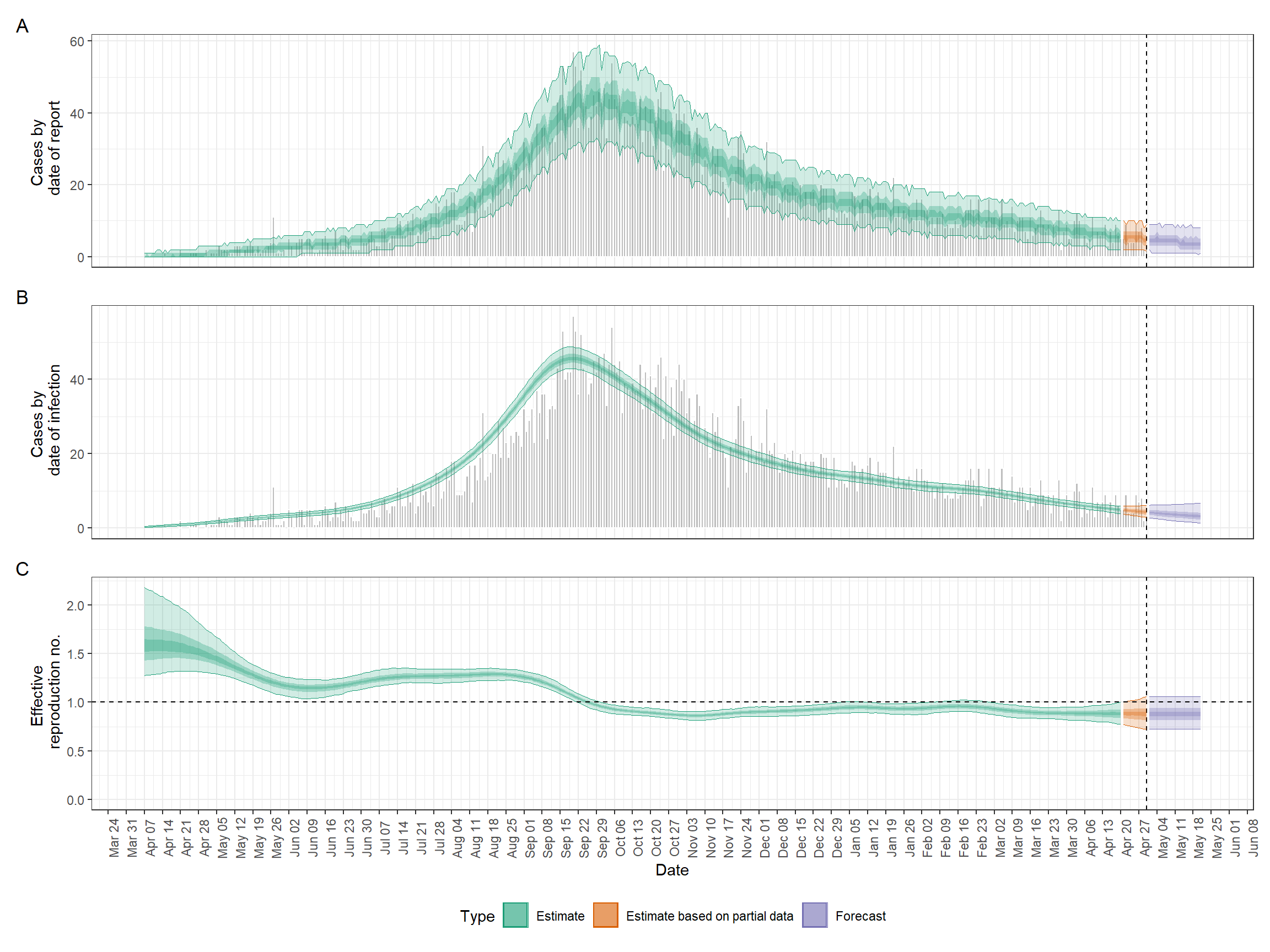
A continuación se muestra un ejemplo de uno de los resultados que produciremos en esta sección.
24.2 Preparación
Utilizaremos dos métodos y paquetes diferentes para la estimación de Rt, a saber, EpiNow y EpiEstim, así como el paquete projections para la previsión de la incidencia de casos.
Este trozo de código muestra la carga de los paquetes necesarios para los análisis. En este manual destacamos p_load() de pacman, que instala el paquete si es necesario y lo carga para su uso. También puedes cargar los paquetes instalados con library() de de R base. Consulta la página sobre fundamentos de R para obtener más información sobre los paquetes de R.
pacman::p_load(
rio, # Importación de ficheros
here, # Localizador de ficheros
tidyverse, # Gestión de datos + gráficos ggplot2
epicontacts, # Análisis de redes de transmisión
EpiNow2, # Estimación Rt
EpiEstim, # Estimación Rt
projections, # Proyecciones de incidencia
incidence2, # Manejo de datos de incidencia
epitrix, # Funciones epi útiles
distcrete # Distribuciones discretas de retraso
)Utilizaremos la lista de casos limpia para todos los análisis de esta sección. Si quieres seguir el proceso, clica para descargar linelist “limpio” (como archivo .rds). Consulta la página de descargando el manual y los datos para descargar todos los datos de ejemplo utilizados en este manual.
# importar linelist depurado
linelist <- import("linelist_cleaned.rds")24.3 Estimación de Rt
EpiNow2 vs. EpiEstim
El número de reproducción R es una medida de la transmisibilidad de una enfermedad y se define como el número esperado de casos secundarios por cada caso infectado. En una población totalmente susceptible, este valor representa el número básico de reproducción R0. Sin embargo, como el número de individuos susceptibles en una población cambia en el transcurso de un brote o pandemia, y como se aplican diversas medidas de respuesta, la medida de transmisibilidad más utilizada es el número de reproducción efectivo Rt; éste se define como el número esperado de casos secundarios por caso infectado en un tiempo t determinado.
El paquete EpiNow2 proporciona el marco más sofisticado para estimar Rt. Tiene dos ventajas clave sobre el otro paquete comúnmente utilizado, EpiEstim:
Tiene en cuenta los retrasos en la notificación y, por lo tanto, puede estimar la Rt incluso cuando los datos recientes son incompletos.
Estima la Rt en función de las fechas de infección y no de las fechas de inicio de la notificación, lo que significa que el efecto de una intervención se reflejará inmediatamente en un cambio en la Rt, en lugar de con un retraso.
Sin embargo, también tiene dos desventajas fundamentales:
Requiere conocer la distribución del tiempo de generación (es decir, la distribución de los retrasos entre la infección de un caso primario y uno secundario), la distribución del periodo de incubación (es decir, la distribución de los retrasos entre la infección y el inicio de los síntomas) y cualquier otra distribución de los retrasos que sea relevante para sus datos (por ejemplo, si tiene fechas de notificación, necesita la distribución de los retrasos desde el inicio de los síntomas hasta la notificación). Aunque esto permitirá una estimación más precisa de Rt, EpiEstim sólo requiere la distribución de intervalos en serie (es decir, la distribución de retrasos entre el inicio de los síntomas de un caso primario y uno secundario), que puede ser la única distribución disponible para usted.
EpiNow2 es significativamente más lento que EpiEstim, anecdóticamente por un factor de 100-1000. Por ejemplo, la estimación de Rt para el brote de la muestra considerada en esta sección tarda unas cuatro horas (esto se ejecutó para un gran número de iteraciones para asegurar una alta precisión y probablemente podría reducirse si fuera necesario, sin embargo los puntos son que el algoritmo es lento en general). Esto puede ser inviable si se actualizan regularmente las estimaciones de Rt.
Por tanto, el paquete que elijas utilizar dependerá de los datos, el tiempo y los recursos informáticos de que disponga.
EpiNow2
Estimación de las distribuciones de los retrasos
Las distribuciones de retraso necesarias para ejecutar EpiNow2 dependen de los datos que tengas. Esencialmente, necesita poder describir el retraso desde la fecha de la infección hasta la fecha del evento que quieres usar para estimar Rt. Si estás usando fechas de inicio, esto sería simplemente la distribución del periodo de incubación. Si se utilizan las fechas de notificación, se requiere el retraso desde la infección hasta la notificación. Como es poco probable que esta distribución se conozca directamente, EpiNow2 permite encadenar varias distribuciones de retraso; en este caso, el retraso desde la infección hasta el inicio de los síntomas (por ejemplo, el periodo de incubación, que probablemente se conoce) y desde el inicio de los síntomas hasta la notificación (que a menudo se puede estimar a partir de los datos).
Como tenemos las fechas de inicio de todos nuestros casos en nuestro linelist de ejemplo, sólo necesitaremos la distribución del periodo de incubación para relacionar nuestros datos (por ejemplo, las fechas de inicio de los síntomas) con la fecha de la infección. Podemos estimar esta distribución a partir de los datos o utilizar valores de la literatura.
Una estimación bibliográfica del periodo de incubación del ébola (tomada de este documento) con una media de 9,1, una desviación estándar de 7,3 y un valor máximo de 30 se especificaría como sigue:
incubation_period_lit <- list(
mean = log(9.1),
mean_sd = log(0.1),
sd = log(7.3),
sd_sd = log(0.1),
max = 30
)Ten en cuenta que EpiNow2 requiere que estas distribuciones de retardo se proporcionen en una escala logarítmica, de ahí la llamada log alrededor de cada valor (excepto el parámetro max que, confusamente, tiene que proporcionarse en una escala natural). Los parámetros mean_sd y sd_sd definen la desviación estándar de las estimaciones de la media y la desviación estándar. Como no se conocen en este caso, elegimos el valor bastante arbitrario de 0,1.
En este análisis, en cambio, estimamos la distribución del periodo de incubación a partir del propio listado utilizando la función bootstrapped_dist_fit, que ajustará una distribución lognormal a los retrasos observados entre la infección y el inicio en linelist.
## estimación del periodo de incubación
incubation_period <- bootstrapped_dist_fit(
linelist$date_onset - linelist$date_infection,
dist = "lognormal",
max_value = 100,
bootstraps = 1
)La otra distribución que necesitamos es el tiempo de generación. Como tenemos datos sobre los tiempos de infección y los enlaces de transmisión, podemos estimar esta distribución a partir de linelist calculando el retraso entre los tiempos de infección de los pares infector-infectado. Para ello, utilizamos la práctica función get_pairwise del paquete epicontacts, que nos permite calcular las diferencias por pares de las propiedades de linelist entre los pares de transmisión. Primero creamos un objeto epicontacts (ver la página de cadenas de transmisión para más detalles):
## generar contactos
contacts <- linelist %>%
transmute(
from = infector,
to = case_id
) %>%
drop_na()
## generar el objeto epicontacts
epic <- make_epicontacts(
linelist = linelist,
contacts = contacts,
directed = TRUE
)A continuación, ajustamos la diferencia de tiempos de infección entre pares de transmisión, calculada mediante get_pairwise, a una distribución gamma:
## estimar el tiempo de generación gamma
generation_time <- bootstrapped_dist_fit(
get_pairwise(epic, "date_infection"),
dist = "gamma",
max_value = 20,
bootstraps = 1
)Ejecución de EpiNow2
Ahora sólo tenemos que calcular la incidencia diaria de linelist, lo que podemos hacer fácilmente con las funciones group_by() y n() de dplyr. Ten en cuenta que EpiNow2 requiere que los nombres de las columnas sean date y confirm.
## obtener la incidencia a partir de las fechas de inicio
cases <- linelist %>%
group_by(date = date_onset) %>%
summarise(confirm = n())Podemos entonces estimar Rt utilizando la función epinow. Algunas notas sobre las entradas:
- Podemos proporcionar cualquier número de distribuciones de retraso “encadenadas” al argumento
delays: simplemente las insertaríamos junto al objetoincubation_perioddentro de la funcióndelay_opts.
- El objeto
return_outputasegura que la salida se devuelve dentro de R y no solo se guarda en un archivo.
-
verboseespecifica que queremos una lectura del progreso. -
horizonindica para cuántos días queremos proyectar la incidencia futura. - Pasamos opciones adicionales al argumento
stanpara especificar durante cuánto tiempo queremos ejecutar la inferencia. Aumentandosamplesychainsobtendremos una estimación más precisa que caracteriza mejor la incertidumbre, sin embargo tardará más en ejecutarse.
## ejecutar epinow
epinow_res <- epinow(
reported_cases = cases,
generation_time = generation_time,
delays = delay_opts(incubation_period),
return_output = TRUE,
verbose = TRUE,
horizon = 21,
stan = stan_opts(samples = 750, chains = 4)
)Análisis de los resultados
Una vez que el código ha terminado de ejecutarse, podemos trazar un resumen muy fácilmente, como se indica a continuación. Desplaza la imagen para ver la extensión completa.
También podemos consultar varias estadísticas resumidas:
## tabla resumen
epinow_res$summary measure estimate
<char> <char>
1: New confirmed cases by infection date 4 (2 -- 6)
2: Expected change in daily cases Unsure
3: Effective reproduction no. 0.88 (0.73 -- 1.1)
4: Rate of growth -0.012 (-0.028 -- 0.0052)
5: Doubling/halving time (days) -60 (130 -- -25)
numeric_estimate
<list>
1: <data.table[1x9]>
2: 0.56
3: <data.table[1x9]>
4: <data.table[1x9]>
5: <data.table[1x9]>Para otros análisis y trazados personalizados, puedes acceder a las estimaciones diarias resumidas a través de $estimates$summarised. Convertiremos esto desde data.table por defecto a un tibble para facilitar su uso con dplyr.
## extraer resumen y convertir a tibble
estimates <- as_tibble(epinow_res$estimates$summarised)
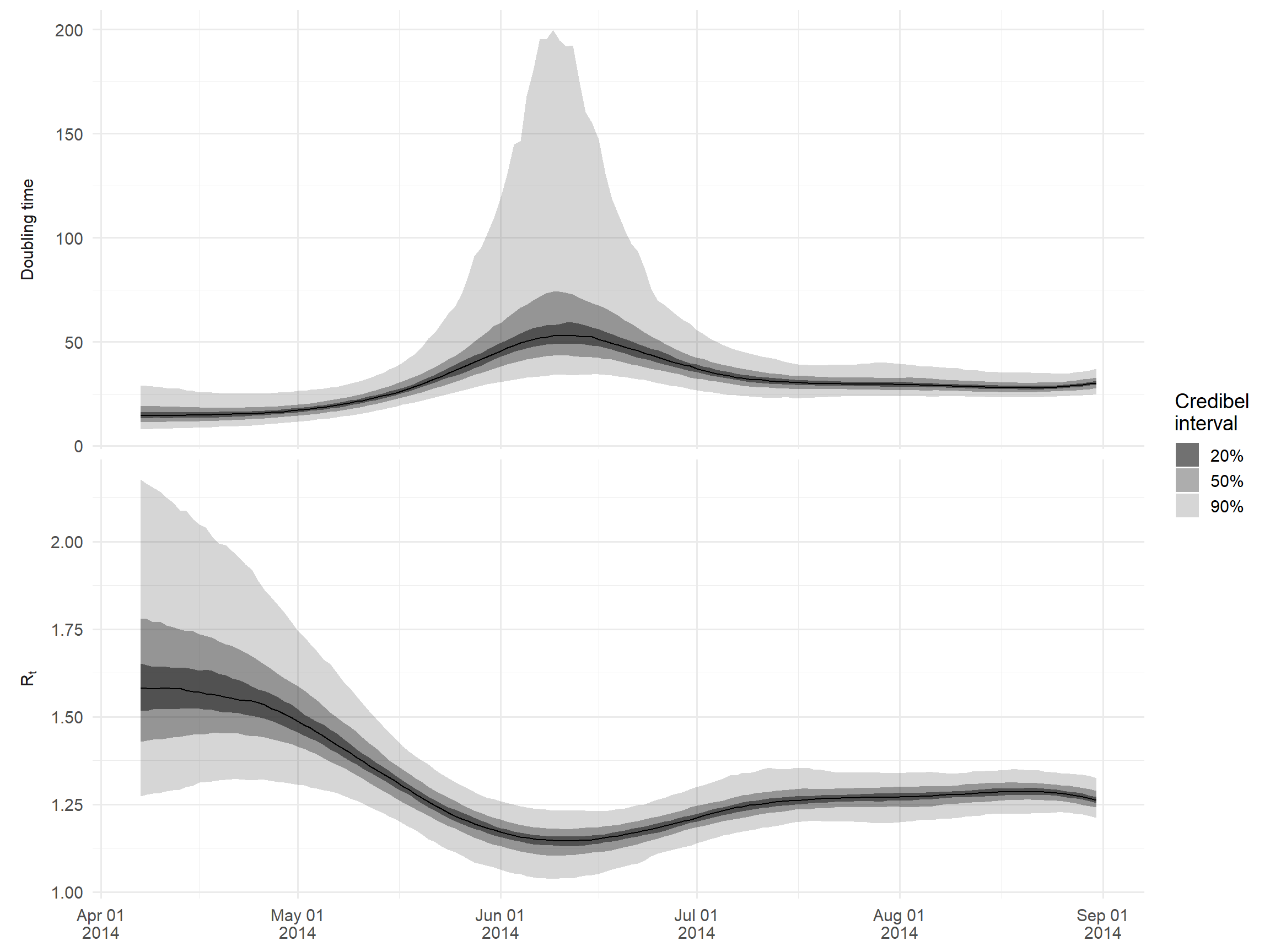
estimatesA modo de ejemplo, hagamos un gráfico del tiempo de duplicación y Rt. Sólo nos fijaremos en los primeros meses del brote, cuando Rt es muy superior a uno, para evitar trazar tiempos de duplicación extremadamente altos.
Utilizamos la fórmula log(2)/growth_rate para calcular el tiempo de duplicación a partir de la tasa de crecimiento estimada.
## hacer un df ancho para el trazado de la mediana
df_wide <- estimates %>%
filter(
variable %in% c("growth_rate", "R"),
date < as.Date("2014-09-01")
) %>%
## convertir las tasas de crecimiento en tiempos de duplicación
mutate(
across(
c(median, lower_90:upper_90),
~ case_when(
variable == "growth_rate" ~ log(2)/.x,
TRUE ~ .x
)
),
## cambiar el nombre de la variable para reflejar la transformación
variable = replace(variable, variable == "growth_rate", "doubling_time")
)
## hacer un df largo para el trazado de cuantiles
df_long <- df_wide %>%
## aquí hacemos coincidir los cuantiles (por ejemplo, lower_90 con upper_90)
pivot_longer(
lower_90:upper_90,
names_to = c(".value", "quantile"),
names_pattern = "(.+)_(.+)"
)
## crear el gráfico
ggplot() +
geom_ribbon(
data = df_long,
aes(x = date, ymin = lower, ymax = upper, alpha = quantile),
color = NA
) +
geom_line(
data = df_wide,
aes(x = date, y = median)
) +
## usar label_parsed para permitir la etiqueta del subscript
facet_wrap(
~ variable,
ncol = 1,
scales = "free_y",
labeller = as_labeller(c(R = "R[t]", doubling_time = "Doubling~time"), label_parsed),
strip.position = 'left'
) +
## definir manualmente la transparencia de los cuantiles
scale_alpha_manual(
values = c(`20` = 0.7, `50` = 0.4, `90` = 0.2),
labels = function(x) paste0(x, "%")
) +
labs(
x = NULL,
y = NULL,
alpha = "Credibel\ninterval"
) +
scale_x_date(
date_breaks = "1 month",
date_labels = "%b %d\n%Y"
) +
theme_minimal(base_size = 14) +
theme(
strip.background = element_blank(),
strip.placement = 'outside'
)EpiEstim
Para ejecutar EpiEstim, necesitamos proporcionar datos sobre la incidencia diaria y especificar el intervalo de serie (es decir, la distribución de los retrasos entre el inicio de los síntomas de los casos primarios y secundarios).
Los datos de incidencia pueden proporcionarse a EpiEstim como un vector, un dataframe o un objeto incidence del paquete incidence original. Incluso se puede distinguir entre infecciones importadas y adquiridas localmente; consulta la documentación en ?estimate_R para más detalles.
Crearemos la entrada utilizando incidence2. Consulta la página sobre curvas epidémicas para ver más ejemplos con el paquete incidence2. Dado que ha habido actualizaciones en el paquete incidence2 que no se alinean completamente con la entrada esperada de estimate_R(), hay algunos pasos adicionales menores necesarios. El objeto incidence consiste en un tibble con fechas y sus respectivos recuentos de casos. Usamos complete() de tidyr para asegurarnos que se incluyen todas las fechas (incluso las que no tienen casos), y luego rename() las columnas para alinearlas con lo que espera estimate_R() en un paso posterior.
## obtener la incidencia a partir de la fecha de inicio
cases <- incidence2::incidence(linelist, date_index = "date_onset") %>% # obtiene el número de casos por día
tidyr::complete(date_index = seq.Date( # asegura que todas las fechas están representadas
from = min(date_index, na.rm = T),
to = max(date_index, na.rm=T),
by = "day"),
fill = list(count = 0)) %>% # convierte los recuentos NA en 0
rename(I = count, # renombra a los nombres esperados por estimateR
dates = date_index)El paquete proporciona varias opciones para especificar el intervalo en serie, cuyos detalles se proporcionan en la documentación en ?estimate_R. Aquí cubriremos dos de ellas.
Utilizando estimaciones de intervalos de serie de la literatura
Utilizando la opción method = "parametric_si", podemos especificar manualmente la media y la desviación estándar del intervalo en serie en un objeto config creado con la función make_config. Utilizamos una media y una desviación estándar de 12,0 y 5,2, respectivamente, definidas en este documento:
## definir config
config_lit <- make_config(
mean_si = 12.0,
std_si = 5.2
)Entonces podemos estimar Rt con la función estimate_R:
cases <- cases %>%
filter(!is.na(date))
#create a dataframe for the function estimate_R()
cases_incidence <- data.frame(dates = seq.Date(from = min(cases$dates),
to = max(cases$dates),
by = 1))
cases_incidence <- left_join(cases_incidence, cases) %>%
select(dates, I) %>%
mutate(I = ifelse(is.na(I), 0, I))Joining with `by = join_by(dates)`epiestim_res_lit <- estimate_R(
incid = cases_incidence,
method = "parametric_si",
config = config_lit
)Default config will estimate R on weekly sliding windows.
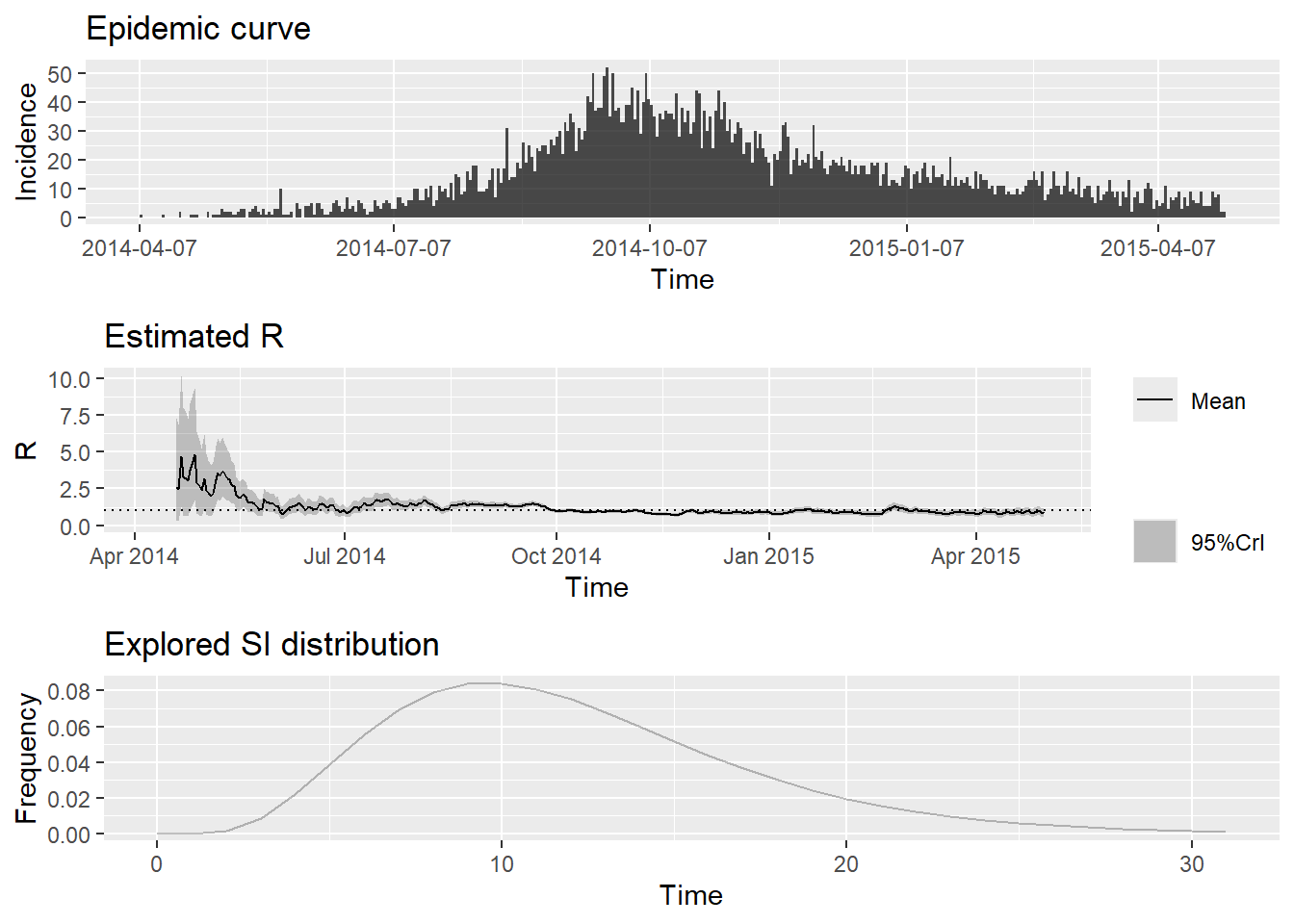
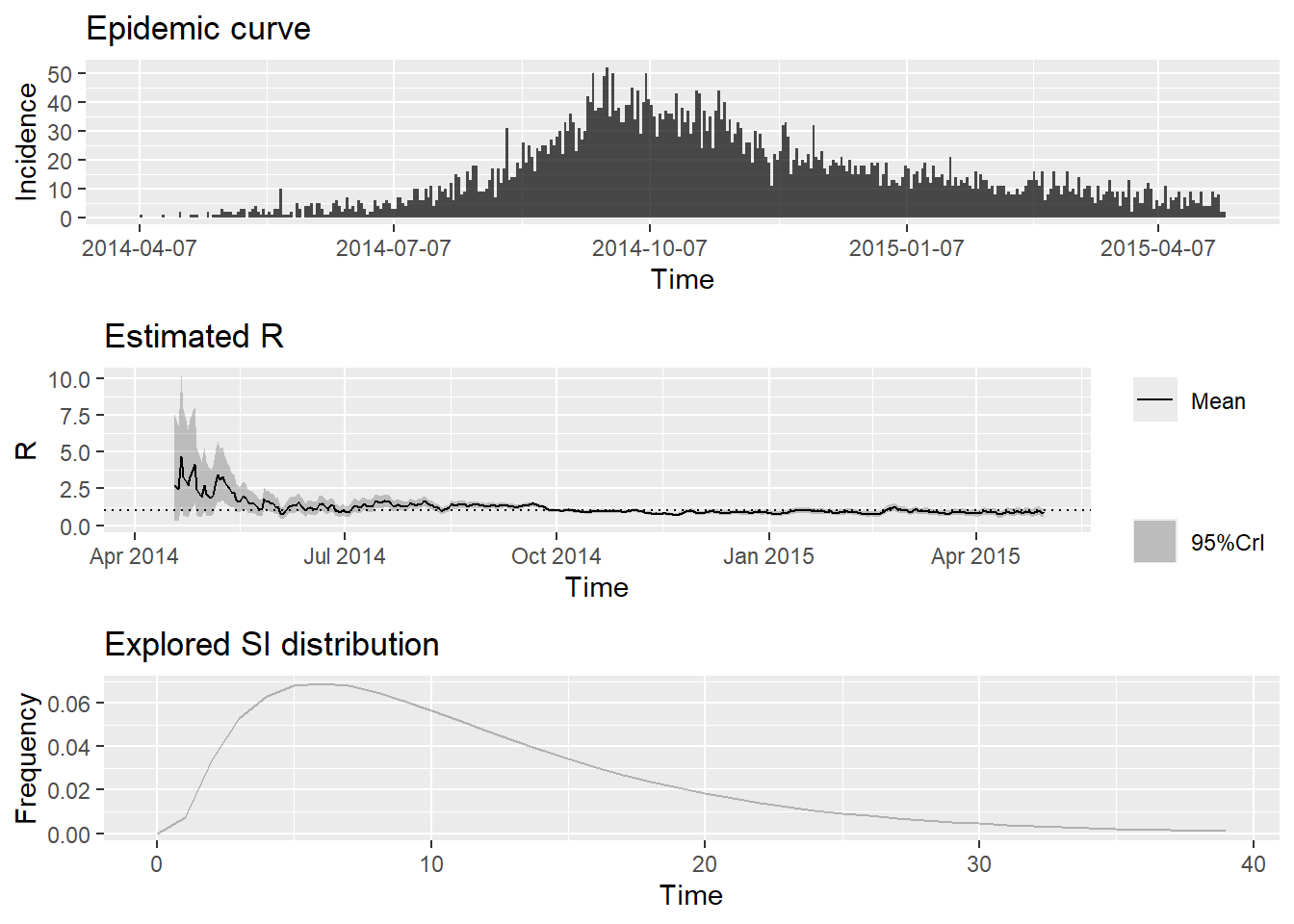
To change this change the t_start and t_end arguments. y trazar un resumen de los resultados:
Utilización de estimaciones de intervalos de serie a partir de los datos
Como tenemos datos sobre las fechas de inicio de los síntomas y los vínculos de transmisión, también podemos estimar el intervalo de serie a partir de linelist calculando el retraso entre las fechas de inicio de los pares infector-infectado. Como hicimos en la sección EpiNow2, utilizaremos la función get_pairwise del paquete epicontacts, que nos permite calcular las diferencias por pares de las propiedades de linelist entre los pares de transmisión. Primero creamos un objeto epicontacts (ver la página de cadenas de transmisión para más detalles):
## generar contactos
contacts <- linelist %>%
transmute(
from = infector,
to = case_id
) %>%
drop_na()
## generar objeto epicontactos
epic <- make_epicontacts(
linelist = linelist,
contacts = contacts,
directed = TRUE
)A continuación, ajustamos la diferencia de fechas de inicio entre los pares de transmisión, calculada mediante get_pairwise, a una distribución gamma. Utilizamos el práctico fit_disc_gamma del paquete epitrix para este procedimiento de ajuste, ya que necesitamos una distribución discreta.
## estimar el intervalo en serie gamma
serial_interval <- fit_disc_gamma(get_pairwise(epic, "date_onset"))A continuación, pasamos esta información al objeto config, ejecutamos de nuevo EpiEstim y trazamos los resultados:
## definir config
config_emp <- make_config(
mean_si = serial_interval$mu,
std_si = serial_interval$sd
)
## ejecutar epiestim
epiestim_res_emp <- estimate_R(
incid = cases_incidence,
method = "parametric_si",
config = config_emp
)Default config will estimate R on weekly sliding windows.
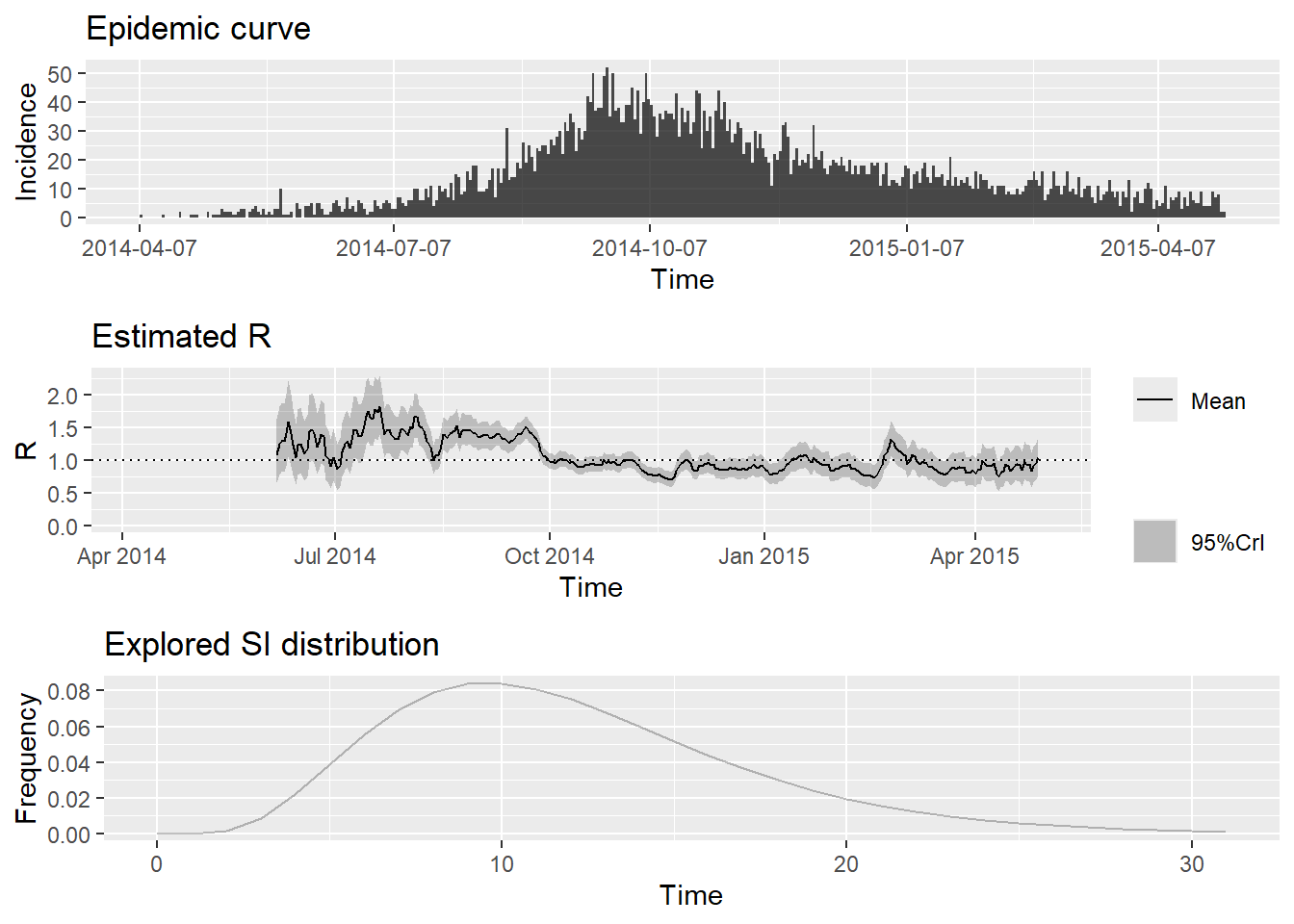
To change this change the t_start and t_end arguments. ## gráfico de resultados
plot(epiestim_res_emp)Especificación de las ventanas de tiempo de estimación
Estas opciones por defecto proporcionarán una estimación deslizante semanal y podrían actuar como una advertencia de que está estimando Rt demasiado pronto en el brote para una estimación precisa. Puedes cambiar esto estableciendo una fecha de inicio posterior para la estimación, como se muestra a continuación. Lamentablemente, EpiEstim sólo proporciona una forma muy tosca de especificar estos tiempos de estimación, ya que tiene que proporcionar un vector de enteros que se refieran a las fechas de inicio y fin de cada ventana temporal.
## definir un vector de fechas a partir del 1 de junio
start_dates <- seq.Date(
as.Date("2014-06-01"),
max(cases$dates) - 7,
by = 1
) %>%
## restar la fecha de inicio para convertirla en numérica
`-`(min(cases$dates)) %>%
## convertir a entero
as.integer()
## añadir seis días para una ventana deslizante de una semana
end_dates <- start_dates + 6
## definir config
config_partial <- make_config(
mean_si = 12.0,
std_si = 5.2,
t_start = start_dates,
t_end = end_dates
)Ahora volvemos a ejecutar EpiEstim y podemos ver que las estimaciones sólo comienzan a partir de junio:
Análisis de los resultados
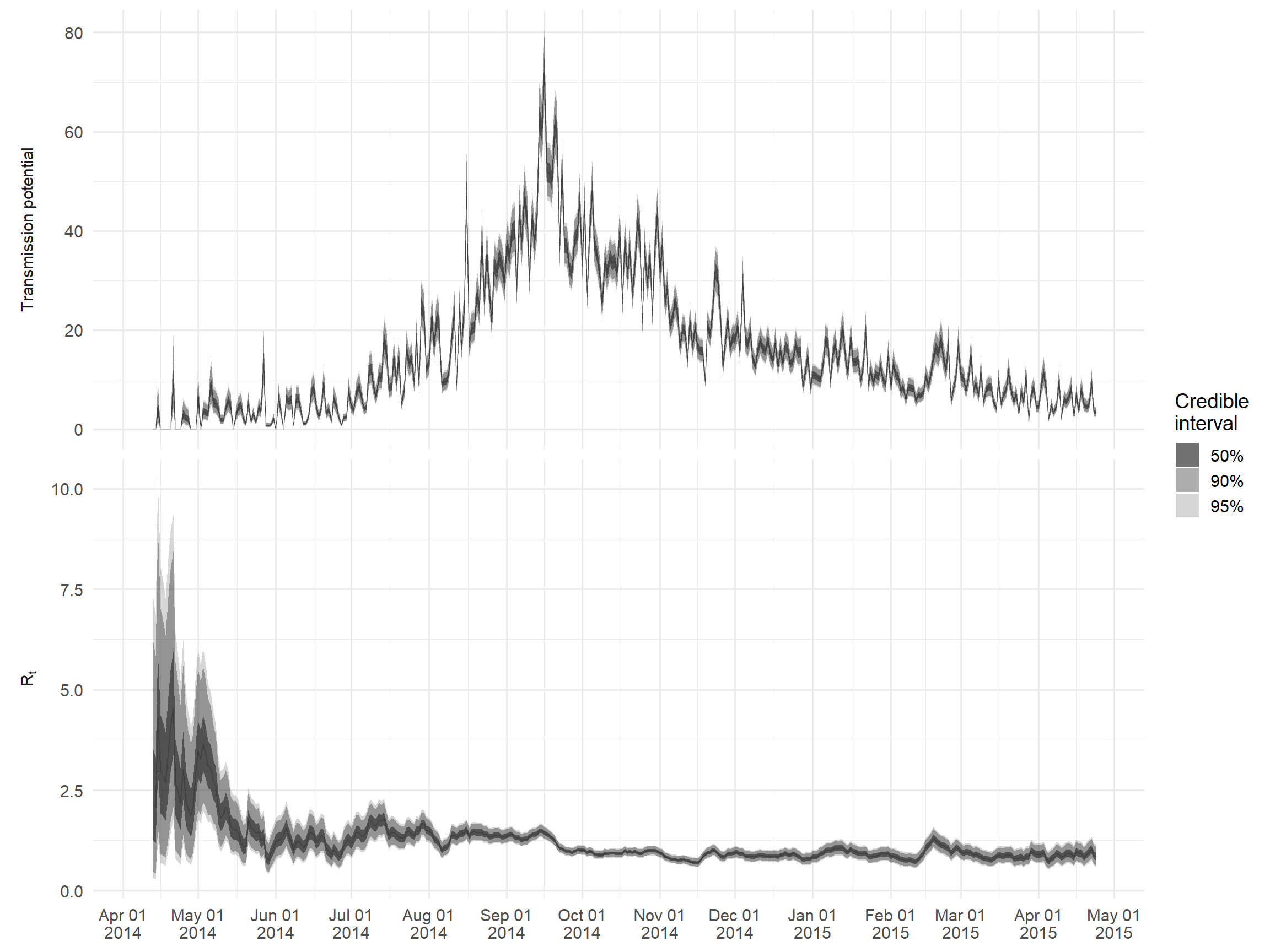
Se puede acceder a los principales resultados a través de $R. Como ejemplo, crearemos un gráfico de Rt y una medida de “potencial de transmisión” dada por el producto de Rt y el número de casos notificados en ese día; esto representa el número esperado de casos en la siguiente generación de infección.
## crear un dataframe ancho para la mediana
df_wide <- epiestim_res_lit$R %>%
rename_all(clean_labels) %>%
rename(
lower_95_r = quantile_0_025_r,
lower_90_r = quantile_0_05_r,
lower_50_r = quantile_0_25_r,
upper_50_r = quantile_0_75_r,
upper_90_r = quantile_0_95_r,
upper_95_r = quantile_0_975_r,
) %>%
mutate(
## extraer la fecha mediana de t_start y t_end
dates = epiestim_res_emp$dates[round(map2_dbl(t_start, t_end, median))],
var = "R[t]"
) %>%
## fusionar los datos de incidencia diaria
left_join(cases, "dates") %>%
## calcular el riesgo en todas las estimaciones de r
mutate(
across(
lower_95_r:upper_95_r,
~ .x*I,
.names = "{str_replace(.col, '_r', '_risk')}"
)
) %>%
## separar las estimaciones de r y las estimaciones de riesgo
pivot_longer(
contains("median"),
names_to = c(".value", "variable"),
names_pattern = "(.+)_(.+)"
) %>%
## asignar niveles de factor
mutate(variable = factor(variable, c("risk", "r")))
## crear un dataframe largo a partir de los cuantiles
df_long <- df_wide %>%
select(-variable, -median) %>%
## seperate r/risk estimates and quantile levels
pivot_longer(
contains(c("lower", "upper")),
names_to = c(".value", "quantile", "variable"),
names_pattern = "(.+)_(.+)_(.+)"
) %>%
mutate(variable = factor(variable, c("risk", "r")))
## realizar gráfico
ggplot() +
geom_ribbon(
data = df_long,
aes(x = dates, ymin = lower, ymax = upper, alpha = quantile),
color = NA
) +
geom_line(
data = df_wide,
aes(x = dates, y = median),
alpha = 0.2
) +
## usar label_parsed para permitir el subíndice label
facet_wrap(
~ variable,
ncol = 1,
scales = "free_y",
labeller = as_labeller(c(r = "R[t]", risk = "Transmission~potential"), label_parsed),
strip.position = 'left'
) +
## definir manualmente la transparencia de los cuantiles
scale_alpha_manual(
values = c(`50` = 0.7, `90` = 0.4, `95` = 0.2),
labels = function(x) paste0(x, "%")
) +
labs(
x = NULL,
y = NULL,
alpha = "Credible\ninterval"
) +
scale_x_date(
date_breaks = "1 month",
date_labels = "%b %d\n%Y"
) +
theme_minimal(base_size = 14) +
theme(
strip.background = element_blank(),
strip.placement = 'outside'
)24.4 Proyección de la incidencia
EpiNow2
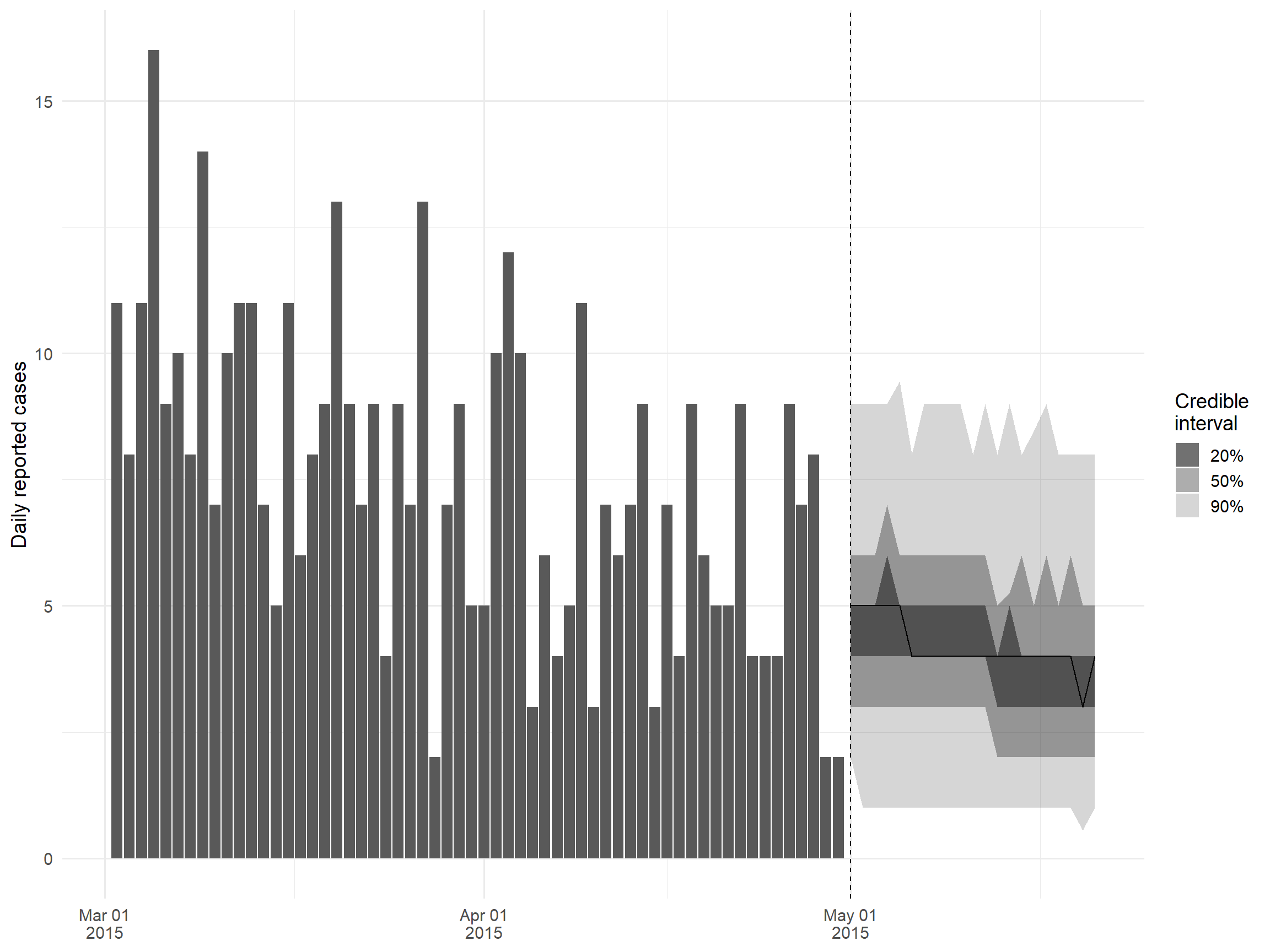
Además de la estimación de Rt, EpiNow2 también admite la previsión de Rt y las proyecciones del número de casos mediante la integración con el paquete EpiSoon por debajo. Todo lo que hay que hacer es especificar el argumento de horizon en la llamada a la función epinow, indicando cuántos días se quiere proyectar en el futuro; véase EpiNow2 en la sección “Estimación de Rt” para obtener detalles sobre cómo poner en marcha EpiNow2. En esta sección, sólo vamos a trazar los resultados de ese análisis, almacenados en el objeto epinow_res.
## definir la fecha mínima para el gráfico
min_date <- as.Date("2015-03-01")
## extraer las estimaciones resumen
estimates <- as_tibble(epinow_res$estimates$summarised)
## extraer datos crudos sobre la incidencia de casos
observations <- as_tibble(epinow_res$estimates$observations) %>%
filter(date > min_date)
## extraer estimaciones previstas del número de casos
df_wide <- estimates %>%
filter(
variable == "reported_cases",
type == "forecast",
date > min_date
)
## convertir a un formato largo para el trazado de cuantiles
df_long <- df_wide %>%
## aquí emparejamos cuantiles coincidentes (por ejemplo, lower_90 con upper_90)
pivot_longer(
lower_90:upper_90,
names_to = c(".value", "quantile"),
names_pattern = "(.+)_(.+)"
)
## hacer el gráfico
ggplot() +
geom_histogram(
data = observations,
aes(x = date, y = confirm),
stat = 'identity',
binwidth = 1
) +
geom_ribbon(
data = df_long,
aes(x = date, ymin = lower, ymax = upper, alpha = quantile),
color = NA
) +
geom_line(
data = df_wide,
aes(x = date, y = median)
) +
geom_vline(xintercept = min(df_long$date), linetype = 2) +
## definir manualmente la transparencia de los cuantiles
scale_alpha_manual(
values = c(`20` = 0.7, `50` = 0.4, `90` = 0.2),
labels = function(x) paste0(x, "%")
) +
labs(
x = NULL,
y = "Daily reported cases",
alpha = "Credible\ninterval"
) +
scale_x_date(
date_breaks = "1 month",
date_labels = "%b %d\n%Y"
) +
theme_minimal(base_size = 14)Proyecciones
El paquete projections desarrollado por RECON hace que sea muy fácil hacer previsiones de incidencia a corto plazo, requiriendo sólo el conocimiento del número de reproducción efectivo Rt y el intervalo serial. Aquí cubriremos cómo utilizar las estimaciones del intervalo de serie de la literatura y cómo utilizar nuestras propias estimaciones de linelist.
Utilizando estimaciones de intervalos de serie de la literatura
Las proyecciones requieren una distribución de intervalos seriales discretizados del tipo distcrete del paquete distcrete. Utilizaremos una distribución gamma con una media de 12,0 y una desviación estándar de 5,2 definida en este documento. Para convertir estos valores en los parámetros de forma y escala necesarios para una distribución gamma, utilizaremos la función gamma_mucv2shapescale del paquete epitrix.
## obtener parámetros de forma y escala a partir de la media mu y el coeficiente de
## variación (por ejemplo, la relación entre la desviación estándar y la media)
shapescale <- epitrix::gamma_mucv2shapescale(mu = 12.0, cv = 5.2/12)
## crear un objeto discreto
serial_interval_lit <- distcrete::distcrete(
name = "gamma",
interval = 1,
shape = shapescale$shape,
scale = shapescale$scale
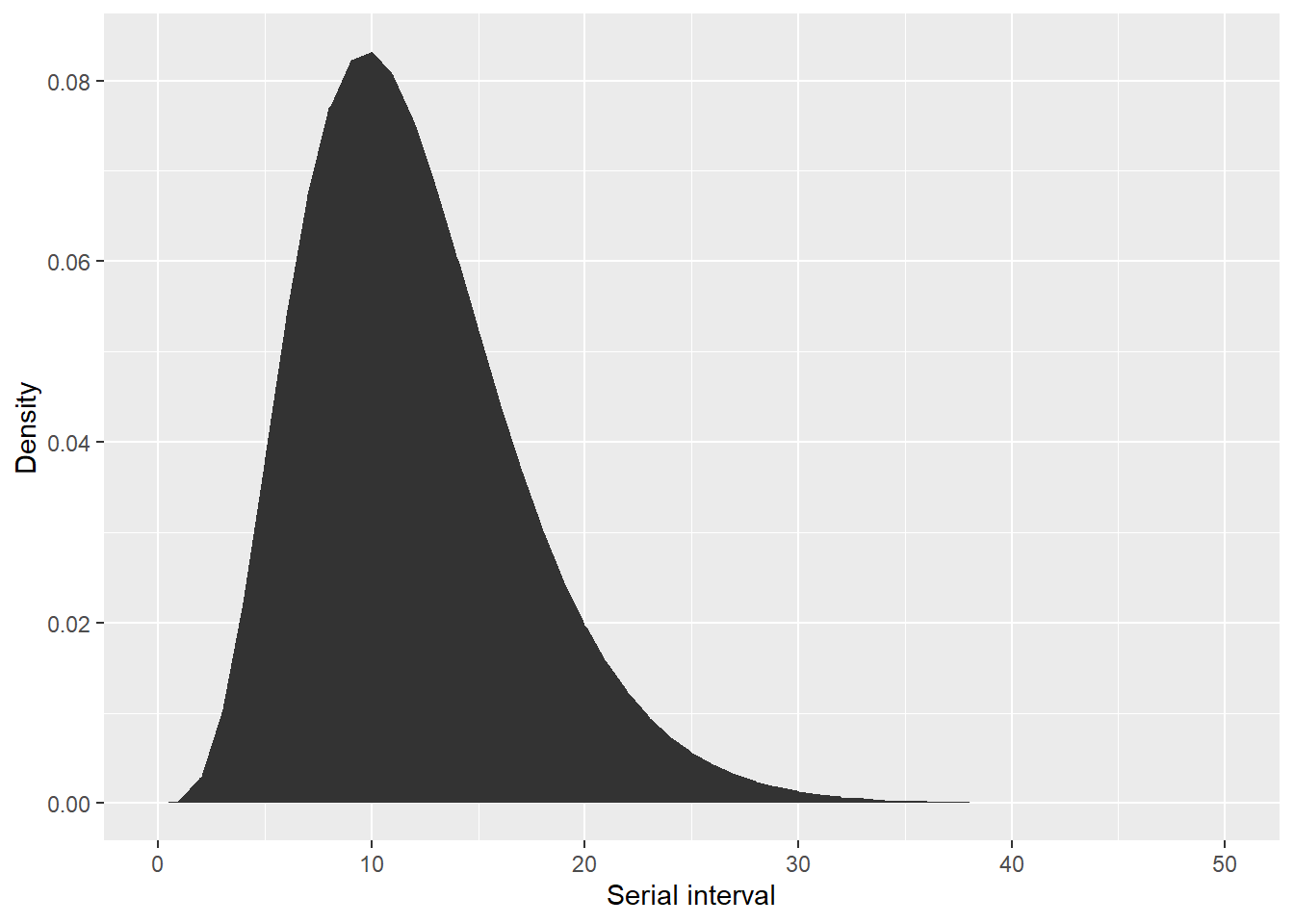
)Aquí tenemos una comprobación rápida para asegurarnos que el intervalo de la serie parece correcto. Accedemos a la densidad de la distribución gamma que acabamos de definir mediante $d, lo que equivale a llamar a dgamma:
Utilización de estimaciones de intervalos de serie a partir de los datos
Como tenemos datos sobre las fechas de inicio de los síntomas y los vínculos de transmisión, también podemos estimar el intervalo de serie a partir de linelist calculando el retraso entre las fechas de inicio de los pares infector-infectado. Como hicimos en la sección EpiNow2, utilizaremos la función get_pairwise del paquete epicontacts, que nos permite calcular las diferencias por pares de las propiedades de linelist entre los pares de transmisión. Primero creamos un objeto epicontacts (ver la página de cadenas de transmisión para más detalles):
## generar contactos
contacts <- linelist %>%
transmute(
from = infector,
to = case_id
) %>%
drop_na()
## generar el objeto epicontacts
epic <- make_epicontacts(
linelist = linelist,
contacts = contacts,
directed = TRUE
)A continuación, ajustamos la diferencia de fechas de inicio entre los pares de transmisión, calculada mediante get_pairwise, a una distribución gamma. Utilizamos el práctico fit_disc_gamma del paquete epitrix para este procedimiento de ajuste, ya que necesitamos una distribución discreta.
## estimar intervalo de serie gamma
serial_interval <- fit_disc_gamma(get_pairwise(epic, "date_onset"))
## inspeccionar la estimación
serial_interval[c("mu", "sd")]$mu
[1] 11.51047
$sd
[1] 7.696056Proyección de la incidencia
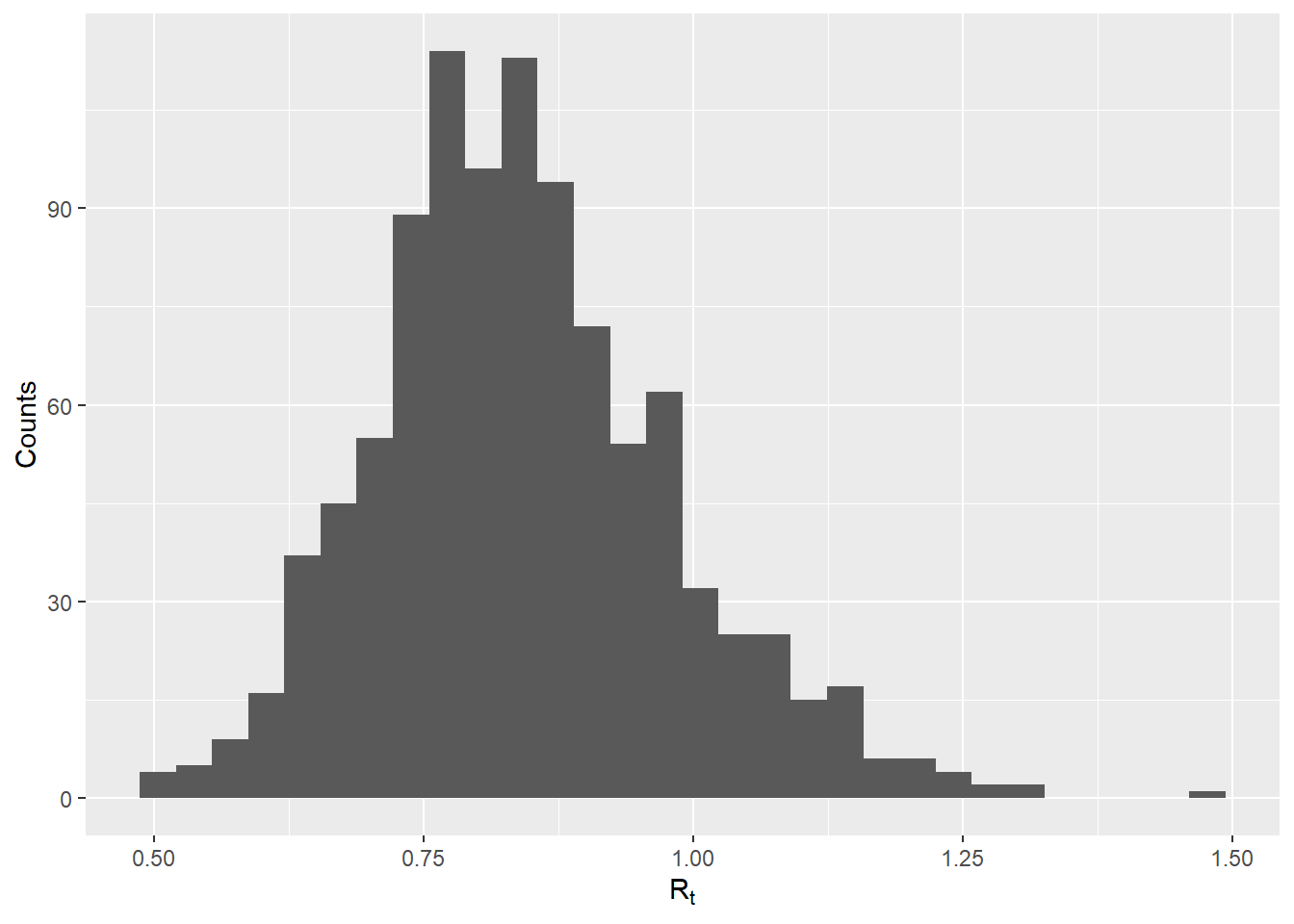
Para proyectar la incidencia futura, todavía tenemos que proporcionar la incidencia histórica en forma de un objeto de incidence, así como una muestra de valores de Rt plausibles. Generaremos estos valores utilizando las estimaciones de Rt generadas por EpiEstim en la sección anterior (en “Estimación de Rt”) y almacenadas en el objeto epiestim_res_emp. En el código siguiente, extraemos las estimaciones de la media y la desviación estándar de Rt para la última ventana temporal del brote (utilizando la función tail para acceder al último elemento de un vector), y simulamos 1000 valores a partir de una distribución gamma utilizando rgamma. También puedes proporcionar un vector propio de valores de Rt que desees utilizar para las proyecciones a futuro.
## crear un objeto de incidencia a partir de las fechas de inicio
inc <- incidence::incidence(linelist$date_onset)256 missing observations were removed.## extraer valores plausibles de r a partir de la estimación más reciente
mean_r <- tail(epiestim_res_emp$R$`Mean(R)`, 1)
sd_r <- tail(epiestim_res_emp$R$`Std(R)`, 1)
shapescale <- gamma_mucv2shapescale(mu = mean_r, cv = sd_r/mean_r)
plausible_r <- rgamma(1000, shape = shapescale$shape, scale = shapescale$scale)
## comprobar la distribución
qplot(x = plausible_r, geom = "histogram", xlab = expression(R[t]), ylab = "Counts")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.A continuación, utilizamos la función project() para realizar la previsión real. Especificamos para cuántos días queremos proyectar mediante los argumentos n_days, y especificamos el número de simulaciones utilizando el argumento n_sim.
## hacer la proyección
proj <- project(
x = inc,
R = plausible_r,
si = serial_interval$distribution,
n_days = 21,
n_sim = 1000
)A continuación, podemos trazar fácilmente la incidencia y las proyecciones utilizando las funciones plot() y add_projections(). Podemos fácilmente subconjuntar el objeto de incidencia para mostrar sólo los casos más recientes utilizando el operador de corchetes.
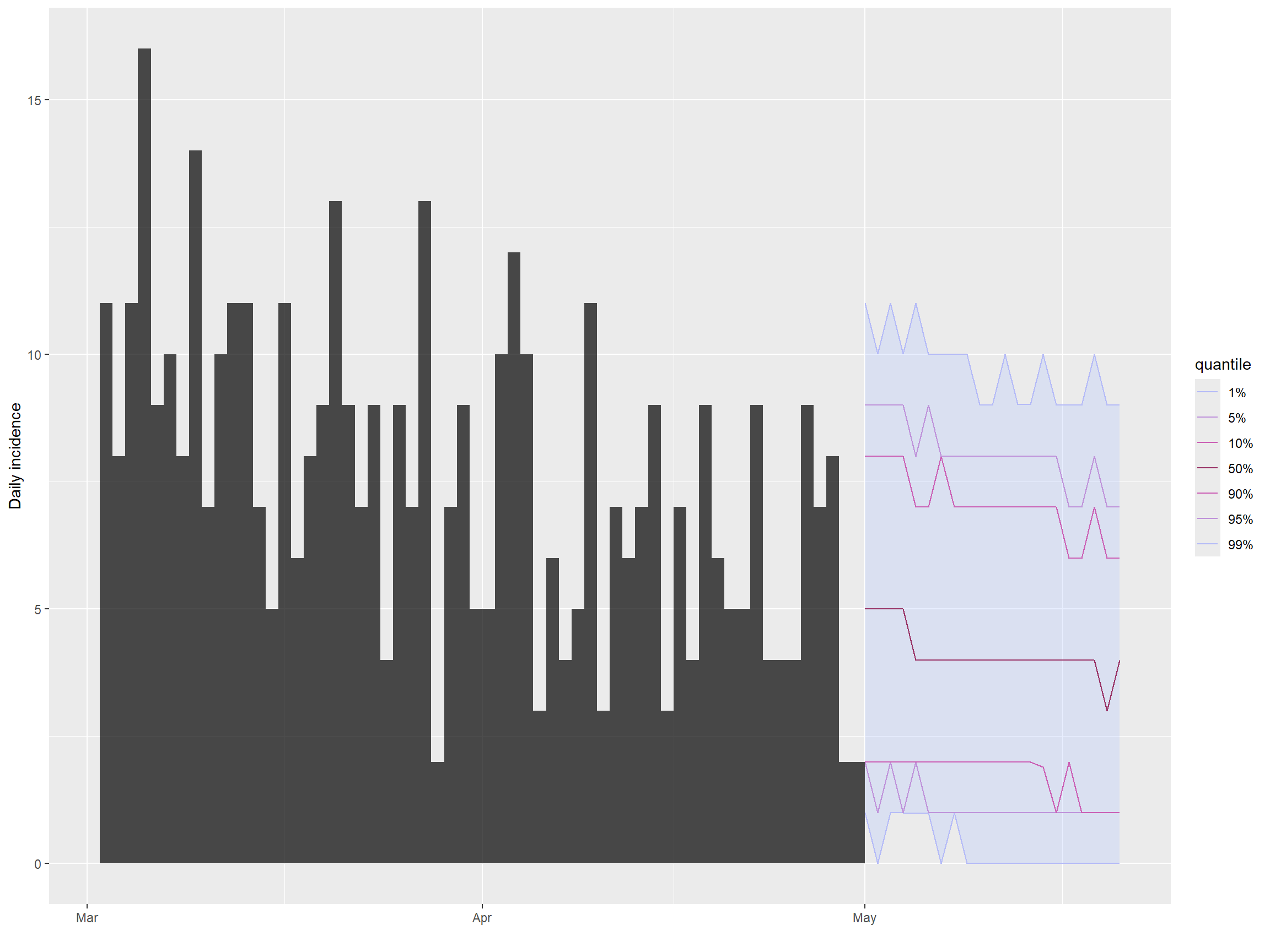
## gráfica de incidencia y proyecciones
plot(inc[inc$dates > as.Date("2015-03-01")]) %>%
add_projections(proj)También puedes extraer fácilmente las estimaciones brutas del número de casos diarios convirtiendo la salida en un dataframe.
## convertir a dataframe para datos crudos
proj_df <- as.data.frame(proj)
proj_df24.5 Recursos
Aquí está el documento que describe la metodología implementada en EpiEstim.
Aquí está el documento que describe la metodología implementada en EpiNow2.
Aquí hay un documento que describe varias consideraciones metodológicas y prácticas para estimar el Rt.