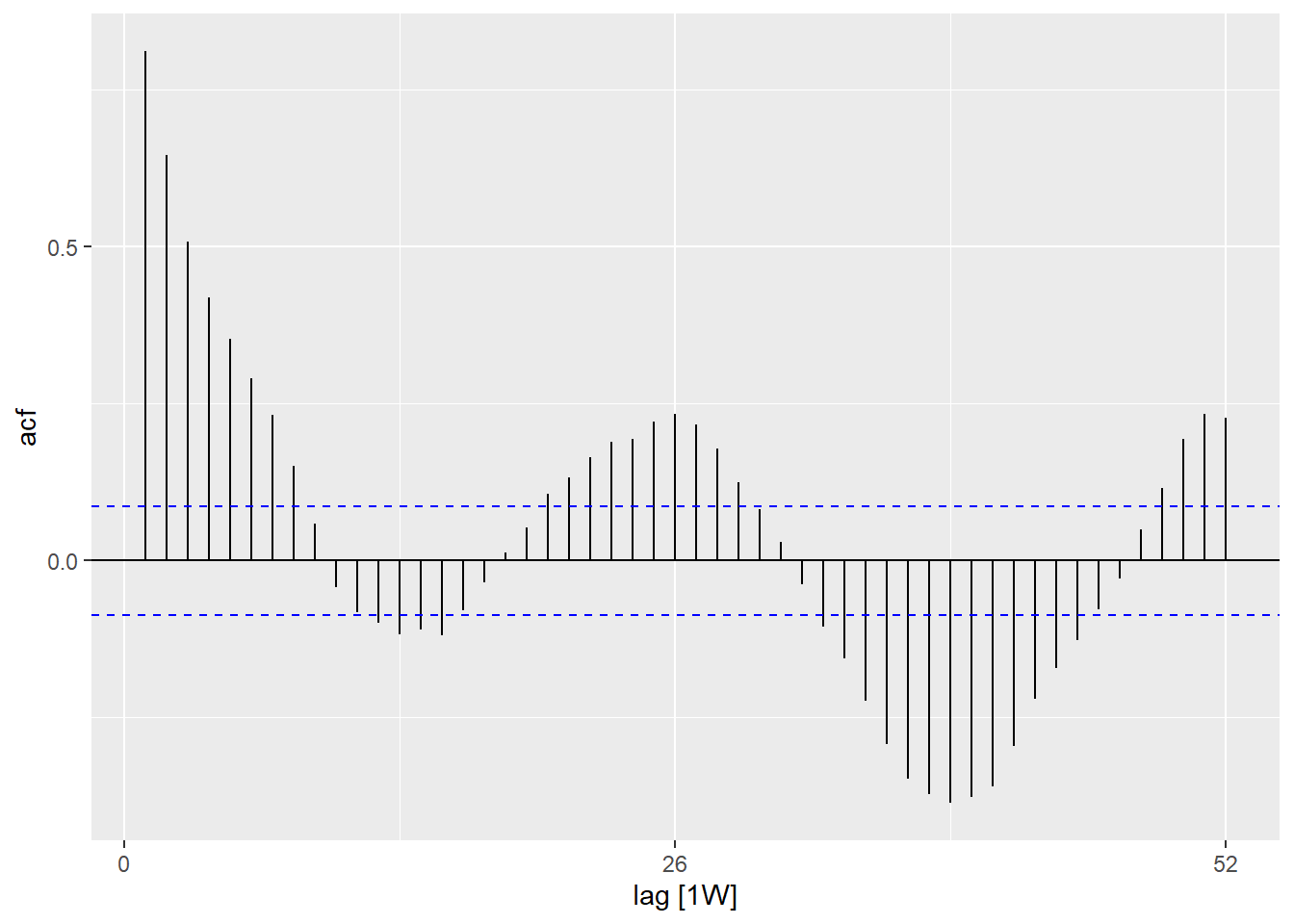pacman::p_load(rio, # Importación de fichero
here, # Localizador de archivos
tidyverse, # gestión de datos + gráficos ggplot2
tsibble, # manejar conjuntos de datos de series temporales
slider, # para calcular medias móviles
imputeTS, # para rellenar valores perdidos
feasts, # para descomposición de series temporales y autocorrelación
forecast, # ajustar los términos sin y cosin a los datos (nota: debe cargarse después de feasts)
trending, # ajustar y evaluar modelos
tmaptools, # para obtener geocoordenadas (lon/lat) basadas en nombres de lugares
ecmwfr, # para interactuar con copernicus sateliate CDS API
stars, # para leer archivos .nc (datos climáticos)
units, # para definir unidades de medida (datos climáticos)
yardstick, # para ver la precisión del modelo
surveillance # para detectar aberraciones
)23 Series temporales y detección de brotes
23.1 Resumen
Esta página muestra el uso de varios paquetes para el análisis de series temporales. Principalmente se basa en paquetes de la familia tidyverts, pero también utilizará el paquete de RECON trending para ajustar modelos más apropiados para la epidemiología de enfermedades infecciosas.
Ten en cuenta que en el siguiente ejemplo utilizamos unos datos del paquete surveillance sobre Campylobacter en Alemania (véase el capítulo Descargando el manual y los datoss del manual para más detalles). Sin embargo, si deseas ejecutar el mismo código en unos datos con múltiples países u otros estratos, hay una plantilla de código de ejemplo para esto en el repo de github de r4epis.
Los temas que se tratan son:
- Datos de series temporales
- Análisis descriptivo
- Ajuste de regresiones
- Relación de dos series temporales
- Detección de brotes
- Series temporales interrumpidas
23.2 Preparación
Paquetes
Este trozo de código muestra la carga de los paquetes necesarios para los análisis. En este manual destacamos p_load() de pacman, que instala el paquete si es necesario y lo carga para su uso. También se pueden cargar paquetes con library() de R base. Consulta la página sobre fundamentos de R para obtener más información sobre los paquetes de R.
Cargar datos
Puedes descargar todos los datos utilizados en este manual mediante las instrucciones de la página de descargando el manual y los datos.
Los datos de ejemplo utilizado en esta sección son los recuentos semanales de casos de campylobacter notificados en Alemania entre 2001 y 2011. Puedes clicar aquí para descargar este archivo de datos (.xlsx).
Este conjunto de datos es una versión reducida de los datos disponibles en el paquete surveillance. (para más detalles, carga el paquete surveillance y consulta ?campyDE)
Importa estos datos con la función import() del paquete rio (maneja muchos tipos de archivos como .xlsx, .csv, .rds - Mira la página de importación y exportación para más detalles).
# importar los recuentos a R
counts <- rio::import("campylobacter_germany.xlsx")A continuación se muestran las 10 primeras filas de los recuentos.
Limpiar datos
El código siguiente se asegura de que la columna de la fecha tenga el formato adecuado. Para esta sección utilizaremos el paquete tsibble y la función yearweek se utilizará para crear una variable de semana de calendario. Hay otras maneras de hacer esto (ver la página de Trabajar con fechas para más detalles), sin embargo para las series temporales es mejor mantenerse dentro de un marco (tsibble).
## asegura que la columna de fecha tiene el formato apropiado
counts$date <- as.Date(counts$date)
## crea una variable de semana calendario
## ajusta las definiciones ISO de las semanas que empiezan en lunes
counts <- counts %>%
mutate(epiweek = yearweek(date, week_start = 1))Descargar datos climáticos
En la sección de relación de dos series temporales, compararemos los recuentos de casos de campylobacter con los datos climáticos.
Los datos climáticos de cualquier parte del mundo pueden descargarse del satélite Copérnico de la UE. No se trata de mediciones exactas, sino que se basan en un modelo (similar a la interpolación), pero la ventaja es la cobertura horaria global, así como las previsiones.
Puedes descargar cada uno de estos archivos de datos climáticos en la página descargando el manual y los datos.
Para propósitos de demostración aquí, mostraremos el código R para usar el paquete ecmwfr para extraer estos datos del almacén de datos climáticos de Copernicus. Es necesario crear una cuenta gratuita para que esto funcione. El sitio web del paquete tiene una guía útil de cómo hacerlo. A continuación se muestra un código de ejemplo de cómo hacer esto, una vez que tienes las claves de la API adecuada. Tienes que sustituir las X de abajo por los ID de tu cuenta. Tendrás que descargar un año de datos a la vez, de lo contrario el servidor se queda sin tiempo.
Si no estás seguro de las coordenadas de un lugar del que quieres descargar datos, puedes utilizar el paquete tmaptools para obtener las coordenadas de OpenStreetMaps. Una opción alternativa es el paquete photon, aunque todavía no se ha publicado en CRAN; lo bueno de photon es que proporciona más datos contextuales para cuando hay varias coincidencias en la búsqueda.
wf_set_key(user = "XXXXX",
key = "XXXXXXXXX-XXXX-XXXX-XXXX-XXXXXXXXXXX",
service = "cds")
## ejecútalo para cada año de interés (de lo contrario, el servidor dejará de funcionar)
for (i in 2002:2011) {
## descargarlos preparando una consulta
## ver aquí cómo hacerlo: https://bluegreen-labs.github.io/ecmwfr/articles/cds_vignette.html#the-request-syntax
## cambia la consulta a una lista usando el botón addin de arriba (python to list)
## ¡¡¡El objetivo es el nombre del fichero de salida!!!
request <- request <- list(
product_type = "reanalysis",
format = "netcdf",
variable = c("2m_temperature", "total_precipitation"),
year = c(i),
month = c("01", "02", "03", "04", "05", "06", "07", "08", "09", "10", "11", "12"),
day = c("01", "02", "03", "04", "05", "06", "07", "08", "09", "10", "11", "12",
"13", "14", "15", "16", "17", "18", "19", "20", "21", "22", "23", "24",
"25", "26", "27", "28", "29", "30", "31"),
time = c("00:00", "01:00", "02:00", "03:00", "04:00", "05:00", "06:00", "07:00",
"08:00", "09:00", "10:00", "11:00", "12:00", "13:00", "14:00", "15:00",
"16:00", "17:00", "18:00", "19:00", "20:00", "21:00", "22:00", "23:00"),
area = request_coords,
dataset_short_name = "reanalysis-era5-single-levels",
target = paste0("germany_weather", i, ".nc")
)
## descargar el archivo y almacenarlo en el directorio de trabajo actual
file <- wf_request(user = "XXXXX", # ID de usuario (para autenticación)
request = request, # la petición
transfer = TRUE, # descargar el archivo
path = here::here("data", "Weather")) ## ruta para guardar los datos
}Cargar datos climáticos
Tanto si has descargado los datos climáticos a través de nuestro manual, como si has utilizado el código anterior, ahora deberías tener 10 años de archivos de datos climáticos “.nc” almacenados en la misma carpeta de tu ordenador.
Utiliza el siguiente código para importar estos archivos en R con el paquete stars.
## definir ruta a carpeta del tiempo
file_paths <- list.files(
here::here("data", "time_series", "weather"), # sustituir por la ruta de archivo propia
full.names = TRUE)
## mantener sólo los que tienen el nombre actual de interés
file_paths <- file_paths[str_detect(file_paths, "germany")]
## leer todos los ficheros como un objeto stars
data <- stars::read_stars(file_paths)t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp,
t2m, tp, Una vez importados estos archivos como datos del objeto, los convertiremos en un dataframe.
## cambiar a un dataframe
temp_data <- as_tibble(data) %>%
## añadir variables y corregir unidades
mutate(
## crear una variable de calendario de semana actual
epiweek = tsibble::yearweek(time),
## crear una variable de fecha (inicio de la semana de calendario)
date = as.Date(epiweek),
## cambiar la temperatura de kelvin a celsius
t2m = set_units(t2m, celsius),
## cambiar la precipitación de metros a milímetros
tp = set_units(tp, mm)) %>%
## agrupar por semanas (aunque también se mantiene la fecha)
group_by(epiweek, date) %>%
## obtener la media por semana
summarise(t2m = as.numeric(mean(t2m)),
tp = as.numeric(mean(tp)))`summarise()` has grouped output by 'epiweek'. You can override using the
`.groups` argument.23.3 Datos de series temporales
Existen varios paquetes para estructurar y manejar los datos de las series temporales. Como ya hemos dicho, nos centraremos en la familia de paquetes tidyverts y, por tanto, utilizaremos el paquete tsibble para definir nuestro objeto de serie temporal. Tener unos datos definidos como objeto de serie temporal significa que es mucho más fácil estructurar nuestro análisis.
Para ello utilizamos la función tsibble() y especificamos el “índex”, es decir, la variable que especifica la unidad de tiempo de interés. En nuestro caso se trata de la variable epiweek.
Si tuviéramos unos datos con recuentos semanales por provincia, por ejemplo, también podríamos especificar la variable de agrupación utilizando el argumento key =. Esto nos permitiría hacer un análisis para cada grupo.
## definir el objeto de serie temporal
counts <- tsibble(counts, index = epiweek)Si observamos el tipo class(counts), veremos que, además de ser un dataframe ordenado (“tbl_df”, “tbl”, “data.frame”), tiene las propiedades adicionales de un dataframe de series temporales (“tbl_ts”).
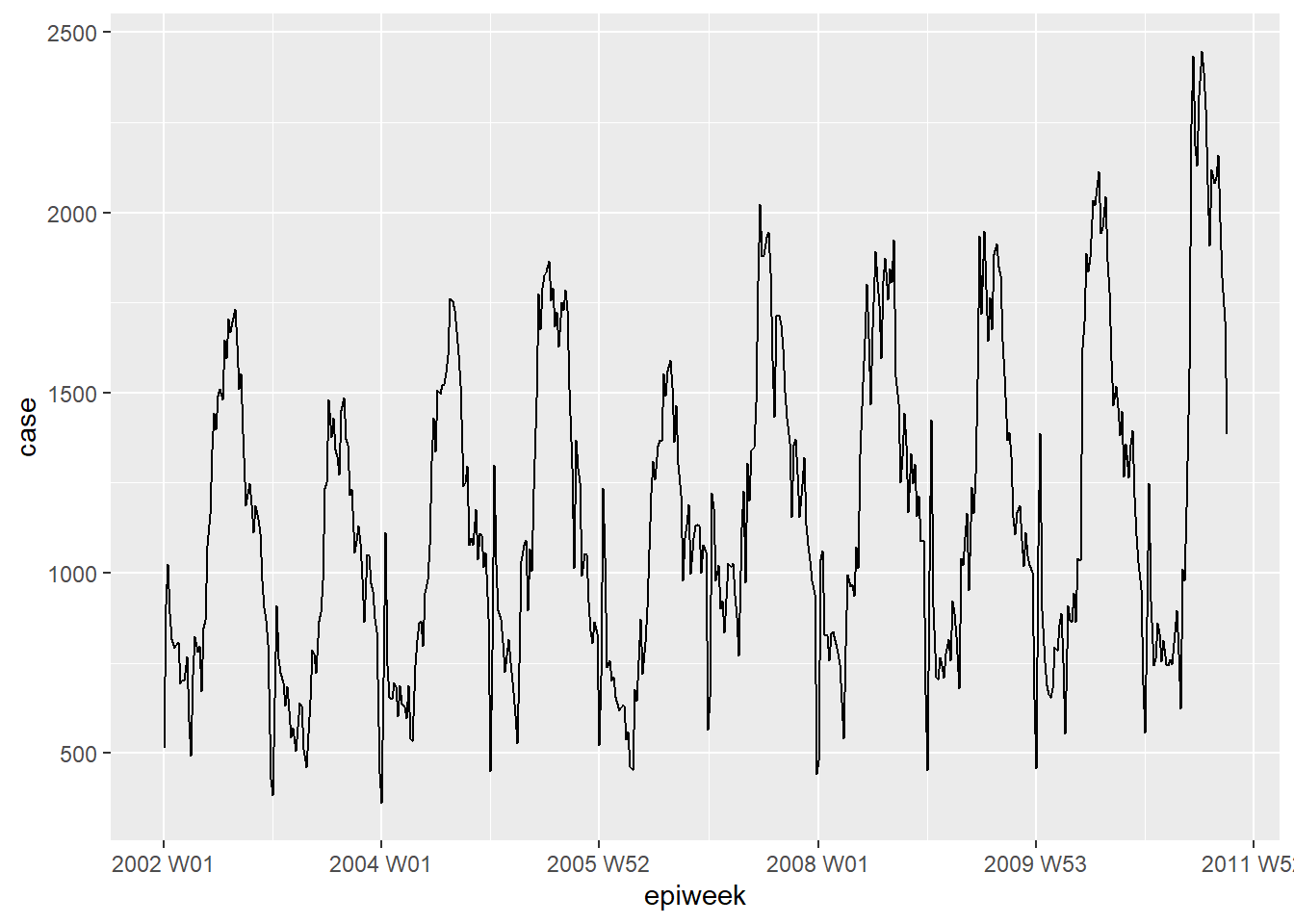
Se puede echar un vistazo rápido a los datos utilizando ggplot2. En el gráfico vemos que hay un claro patrón estacional y que no hay pérdidas. Sin embargo, parece haber un problema con la notificación al principio de cada año; los casos descienden en la última semana del año y luego aumentan en la primera semana del año siguiente.
## trazar un gráfico lineal de casos por semana
ggplot(counts, aes(x = epiweek, y = case)) +
geom_line()PELIGRO: La mayoría de los conjuntos de datos no están tan limpios como este ejemplo. Tendrás que comprobar si hay duplicados y faltas como se indica a continuación.
Duplicados
tsibble no permite observaciones duplicadas. Así que cada fila deberá ser única, o única dentro del grupo (variable key). El paquete tiene algunas funciones que ayudan a identificar los duplicados. Entre ellas se encuentran are_duplicated(), que proporciona un vector TRUE/FALSE para saber si la fila es un duplicado, y duplicates(), que proporciona un dataframe de las filas duplicadas.
Consulta la página sobre De-duplicación para obtener más detalles sobre cómo seleccionar las filas que desees.
## obtener un vector de TRUE/FALSE si las filas están duplicadas
are_duplicated(counts, index = epiweek)
## obtener un data frame de filas duplicadas
duplicates(counts, index = epiweek) Valores faltantes
En nuestra breve inspección anterior hemos visto que no hay faltas, pero también hemos visto que parece haber un problema de retraso en la notificación en torno al año nuevo. Una forma de abordar este problema podría ser establecer estos valores como faltantes y luego imputar los valores. La forma más sencilla de imputación de series temporales consiste en trazar una línea recta entre el último valor no faltante y el siguiente valor no faltante. Para ello, utilizaremos la función na_interpolation() del paquete imputeTS.
Consulta la página de datos faltantes para conocer otras opciones de imputación.
Otra alternativa sería calcular una media móvil para intentar suavizar estos aparentes problemas de información (véase la siguiente sección y la página sobre medias móviles.
## crear una variable con los faltantes en lugar de las semanas con problemas de información
counts <- counts %>%
mutate(case_miss = if_else(
## si epiweek contiene 52, 53, 1 ó 2
str_detect(epiweek, "W51|W52|W53|W01|W02"),
## entonces se establece como missing
NA_real_,
## de lo contrario, mantiene el valor por si acaso
case
))
## alternativamente interpola los faltantes por tendencia lineal
## entre dos puntos adyacentes más cercanos
counts <- counts %>%
mutate(case_int = imputeTS::na_interpolation(case_miss)
)
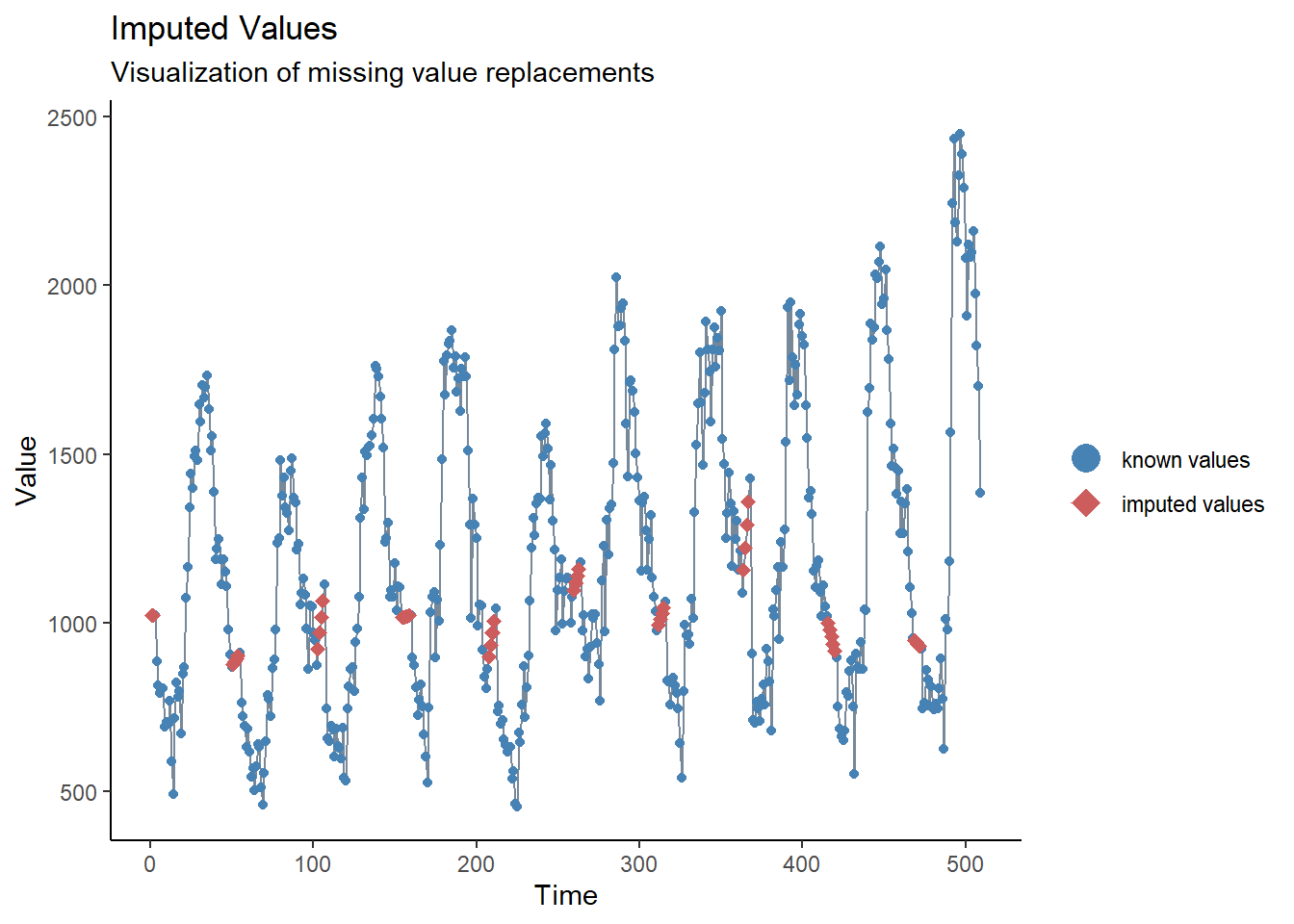
## para comprobar qué valores se han imputado en comparación con el original
ggplot_na_imputations(counts$case_miss, counts$case_int) +
## hacer un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic()23.4 Análisis descriptivo
Medias móviles
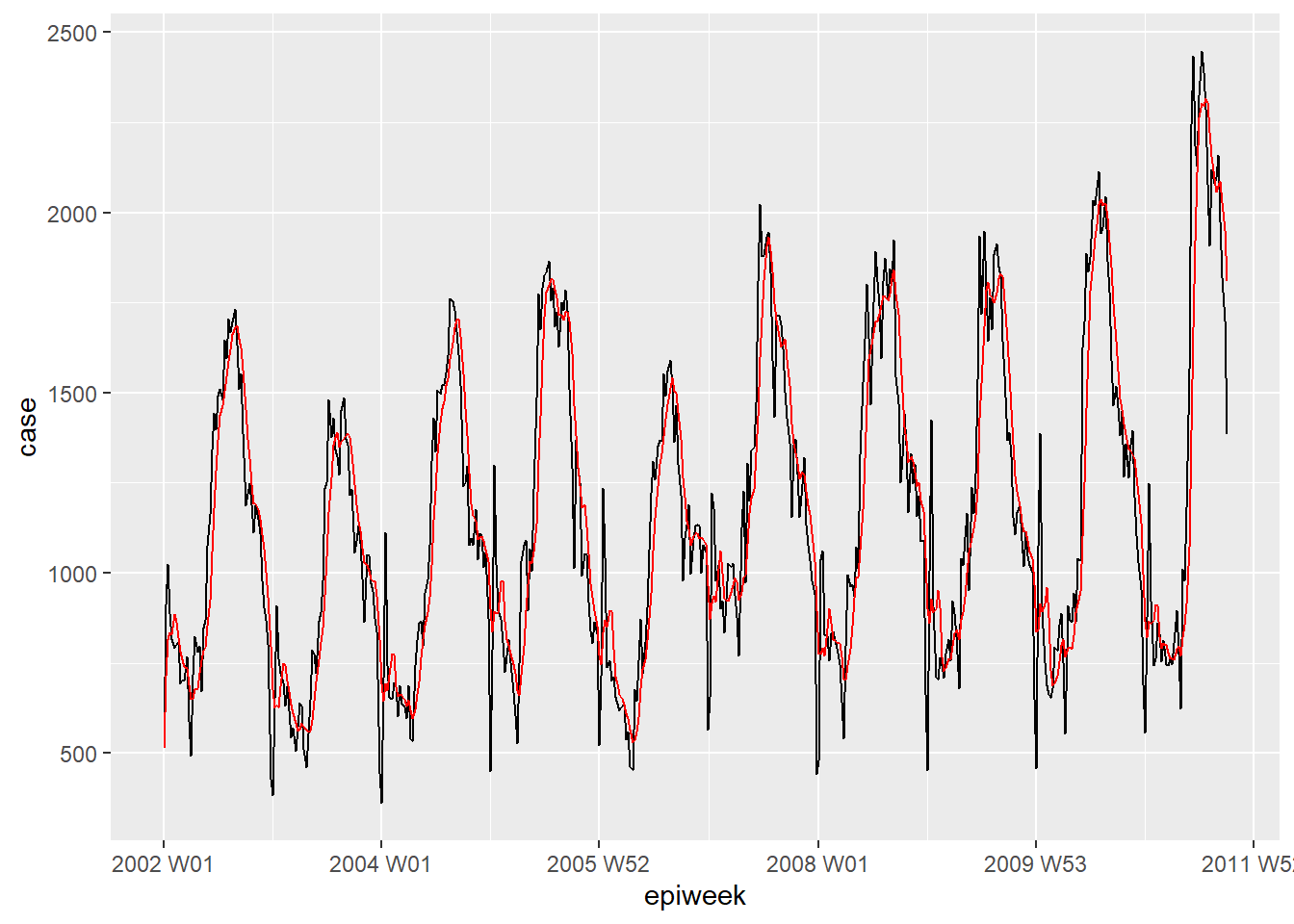
Si los datos tienen mucho ruido (los recuentos suben y bajan), puede ser útil calcular una media móvil. En el ejemplo siguiente, para cada semana se calcula la media de casos de las cuatro semanas anteriores. Esto suaviza los datos para hacerlos más interpretables. En nuestro caso esto no aporta mucho, así que nos quedaremos con los datos interpolados para el análisis posterior. Véase la página de medias móviles para más detalles.
## crear una variable de media móvil (se ocupa de las pérdidas)
counts <- counts %>%
## crear la variable ma_4w
## desplazar sobre cada fila de la variable de caso
mutate(ma_4wk = slider::slide_dbl(case,
## para cada fila calcula el nombre
~ mean(.x, na.rm = TRUE),
## utiliza las cuatro semanas anteriores
.before = 4))
## hacer una visualización rápida de la diferencia
ggplot(counts, aes(x = epiweek)) +
geom_line(aes(y = case)) +
geom_line(aes(y = ma_4wk), colour = "red")Periodicidad
A continuación definimos una función personalizada para crear un periodograma. Consulta la página Escribir funciones para obtener información sobre cómo escribir funciones en R.
En primer lugar, se define la función. Sus argumentos incluyen unos datos con las columnas counts, start_week = que es la primera semana de los datos, un número para indicar cuántos períodos por año (por ejemplo, 52, 12) y, por último, el estilo de salida (véanse los detalles en el código siguiente).
## Argumentos de la función
###########################
## x es un conjunto de datos
## counts es una variable con datos de recuento o tasas dentro de x
## start_week es la primera semana del conjunto de datos
## period es el número de unidades en un año
## output es si quiere devolver el periodograma espectral o las semanas de pico
## "periodogram" o "weeks"
# Define la función
periodogram <- function(x,
counts,
start_week = c(2002, 1),
period = 52,
output = "weeks") {
## asegurarse de que no es un tsibble, filtrar al proyecto y mantener sólo las columnas de interés
prepare_data <- dplyr::as_tibble(x)
# prepare_data <- prepare_data[prepare_data[[strata]] == j, ]
prepare_data <- dplyr::select(prepare_data, {{counts}})
## crear una serie temporal intermedia "zoo" para poder utilizarla con spec.pgram
zoo_cases <- zoo::zooreg(prepare_data,
start = start_week, frequency = period)
## obtener un periodograma espectral sin utilizar la transformada rápida de fourier
periodo <- spec.pgram(zoo_cases, fast = FALSE, plot = FALSE)
## devuelve las semanas de pico
periodo_weeks <- 1 / periodo$freq[order(-periodo$spec)] * period
if (output == "weeks") {
periodo_weeks
} else {
periodo
}
}
## obtener el periodograma espectral para extraer las semanas con las frecuencias más altas
## (comprobación de la estacionalidad)
periodo <- periodogram(counts,
case_int,
start_week = c(2002, 1),
output = "periodogram")
## extraer el espectro y la frecuencia en un dataframe para graficarlo
periodo <- data.frame(periodo$freq, periodo$spec)
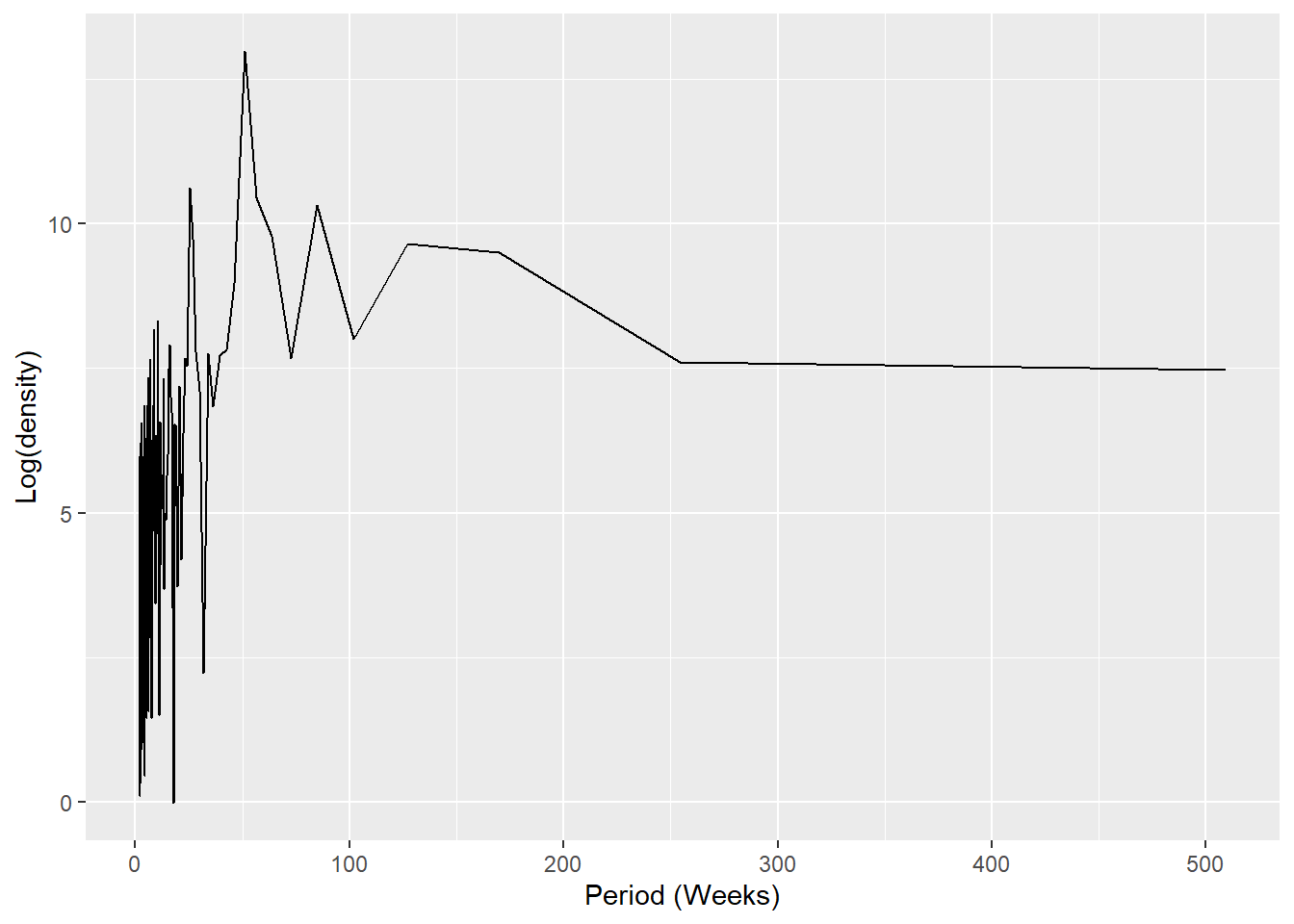
## trazar un periodograma que muestre la periodicidad más frecuente
ggplot(data = periodo,
aes(x = 1/(periodo.freq/52), y = log(periodo.spec))) +
geom_line() +
labs(x = "Period (Weeks)", y = "Log(density)")## obtener un vector semanas en orden ascendente
peak_weeks <- periodogram(counts,
case_int,
start_week = c(2002, 1),
output = "weeks")NOTA: Es posible utilizar las semanas anteriores para añadirlas a los términos del seno y del coseno, sin embargo, utilizaremos una función para generar estos términos (véase la sección de regresión más adelante)
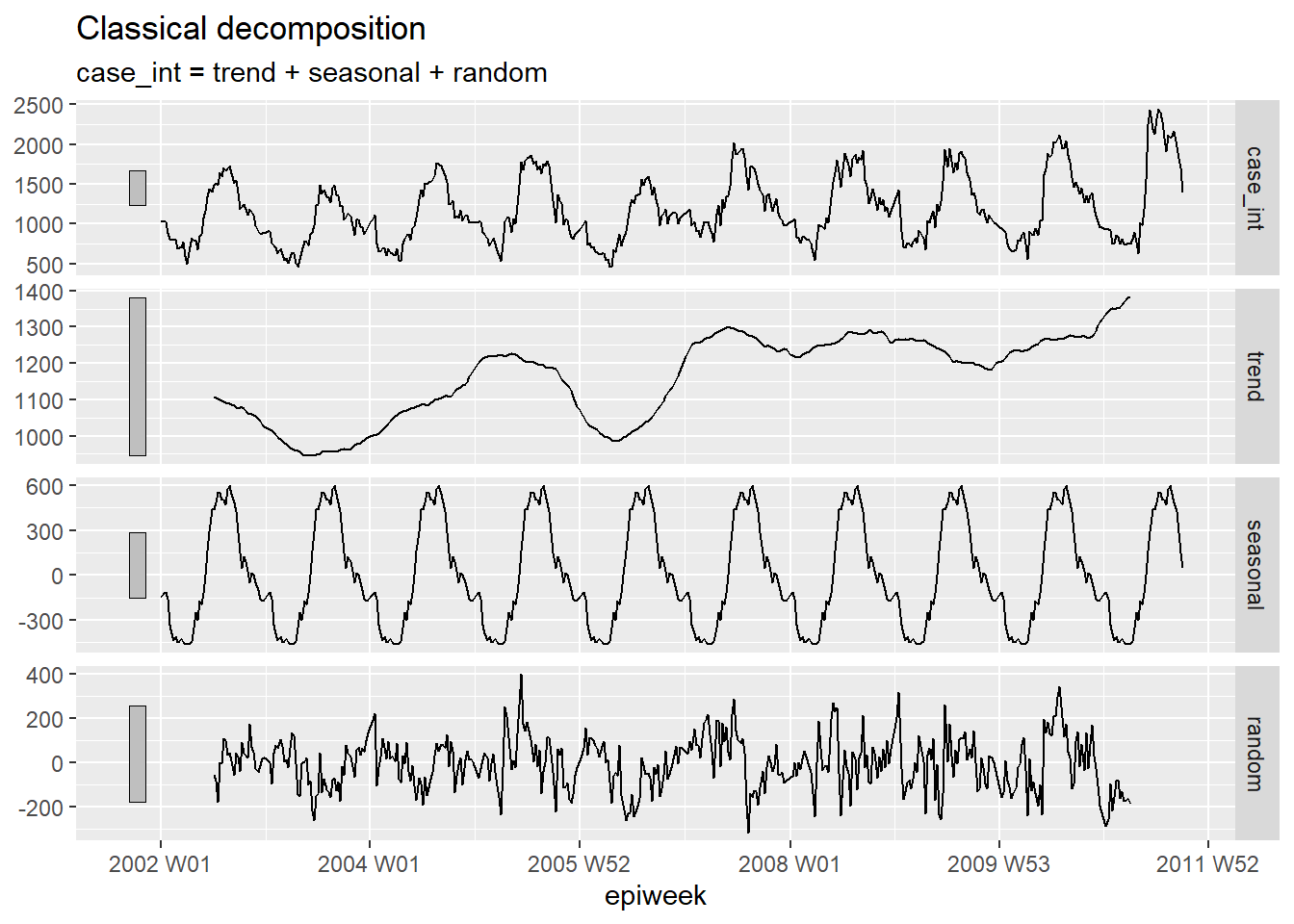
Descomposición
La descomposición clásica se utiliza para desglosar una serie temporal en varias partes, que en conjunto conforman el patrón que se observa. Estas diferentes partes son:
- La tendencia-ciclo (la dirección a largo plazo de los datos)
- La estacionalidad (patrones repetitivos)
- El azar (lo que queda después de quitar la tendencia y la estacionalidad)
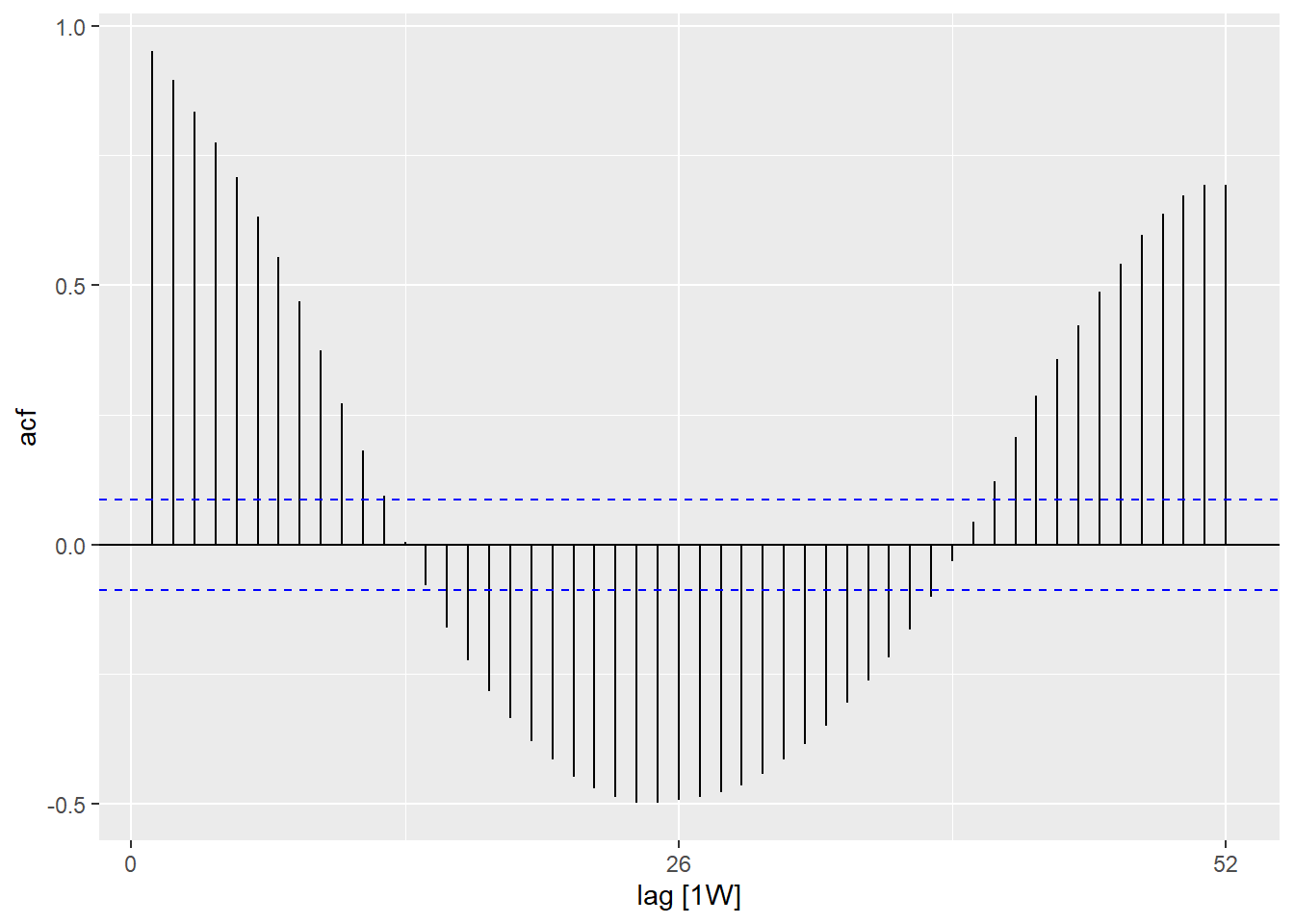
Autocorrelación
La autocorrelación informa de la relación entre los recuentos de cada semana y las semanas anteriores (denominadas retrasos o retardos).
Utilizando la función ACF(), podemos producir un gráfico que nos muestre un número de líneas para la relación en diferentes retrasos. Cuando el retardo es 0 (x = 0), esta línea sería siempre 1, ya que muestra la relación entre una observación y ella misma (no se muestra aquí). La primera línea mostrada aquí (x = 1) muestra la relación entre cada observación y la observación anterior (retardo de 1), la segunda muestra la relación entre cada observación y la observación anterior (retardo de 2) y así sucesivamente hasta el retardo de 52 que muestra la relación entre cada observación y la observación de 1 año (52 semanas antes).
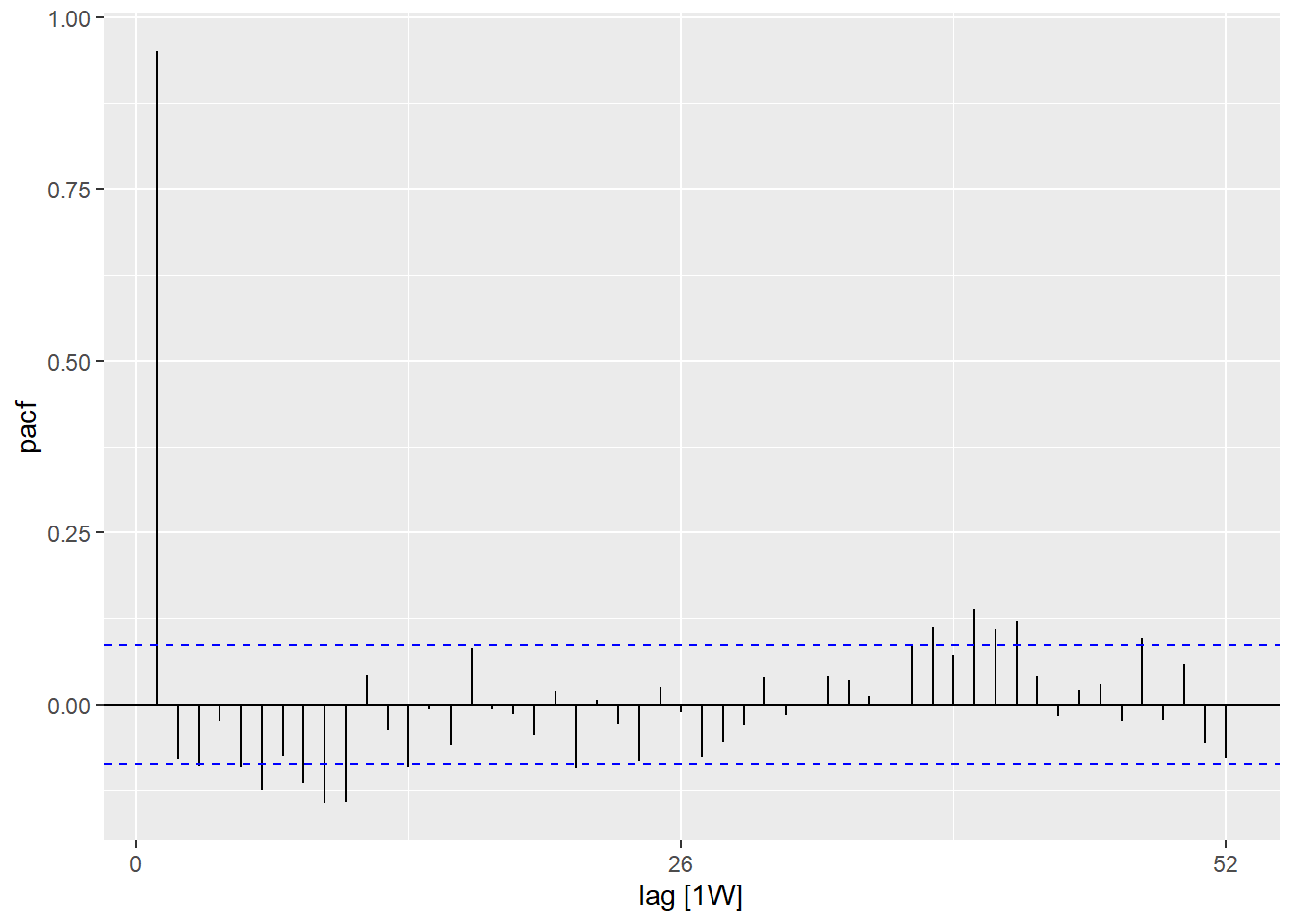
El uso de la función PACF() (para la autocorrelación parcial) muestra el mismo tipo de relación pero ajustada para todas las demás semanas intermedias. Esto es menos informativo para determinar la periodicidad.
## utilizando el conjunto de datos de recuentos
counts %>%
## calcula la autocorrelación utilizando retardos de un año completo
ACF(case_int, lag_max = 52) %>%
## muestra un gráfico
autoplot()## utilizando el conjunto de datos de recuentos
counts %>%
## calcular la autocorrelación parcial utilizando los retardos de un año completo
PACF(case_int, lag_max = 52) %>%
## muestra un gráfico
autoplot()Puedes probar formalmente la hipótesis nula de independencia en una serie temporal (es decir, que no está autocorrelacionada) utilizando la prueba de Ljung-Box (en el paquete stats). Un valor-p significativo sugiere que hay autocorrelación en los datos.
## prueba de independencia
Box.test(counts$case_int, type = "Ljung-Box")
Box-Ljung test
data: counts$case_int
X-squared = 462.65, df = 1, p-value < 2.2e-1623.5 Ajuste de regresiones
Es posible ajustar un gran número de regresiones diferentes a una serie temporal, sin embargo, aquí mostraremos cómo ajustar una regresión binomial negativa, ya que suele ser la más apropiada para los datos de recuento en las enfermedades infecciosas.
Términos de Fourier
Los términos de Fourier son el equivalente a las curvas seno y coseno. La diferencia es que éstos se ajustan basándose en la búsqueda de la combinación de curvas más adecuada para explicar los datos.
Si sólo se ajusta un término de fourier, esto equivaldría a ajustar un seno y un coseno para el desfase más frecuente que se ve en el periodograma (en nuestro caso, 52 semanas). Utilizamos la función fourier() del paquete forecast.
En el código de abajo asignamos usando el $, ya que fourier() devuelve dos columnas (una para seno y otra para el coseno) y así se añaden al conjunto de datos como una lista, llamada “fourier” - pero esta lista se puede usar como una variable normal en la regresión.
## añade los términos de fourier usando las variabless epiweek y case_int
counts$fourier <- select(counts, epiweek, case_int) %>%
fourier(K = 1)Binomial negativa
Es posible ajustar las regresiones utilizando las funciones básicas de stats o MASS (por ejemplo, lm(), glm() y glm.nb()). Sin embargo, utilizaremos las del paquete trending, ya que esto permite calcular intervalos de confianza y predicción adecuados (que de otro modo no están disponibles). La sintaxis es la misma, y se especifica una variable de resultado, luego una tilde (~) y luego se añaden las diversas variables de exposición de interés separadas por un signo más (+).
La otra diferencia es que primero definimos el modelo y luego lo ajustamos a los datos (fit()). Esto es útil porque permite comparar varios modelos diferentes con la misma sintaxis.
SUGERENCIA: Si deseas utilizar tasas, en lugar de recuentos, puedes incluir la variable de población como un término de compensación logarítmica, añadiendo offset(log(population). Entonces tendría que establecerse que la población es 1, antes de usar predict() para producir una tasa.
SUGERENCIA: Para ajustar modelos más complejos, como ARIMA o prophet, consulta el paquete fable
## define el modelo que quieres ajustar (binomial negativo)
model <- glm_nb_model(
## establece el número de casos como resultado de interés
case_int ~
## utiliza epiweek para tener en cuenta la tendencia
epiweek +
## usa los términos de fourier para tener en cuenta la estacionalidad
fourier)
## ajusta tu modelo utilizando el conjunto de datos de recuentos
fitted_model <- trending::fit(model, data.frame(counts))
## calcula los intervalos de confianza y de predicción
observed <- predict(fitted_model, simulate_pi = FALSE)
estimate_res <- data.frame(observed$result)
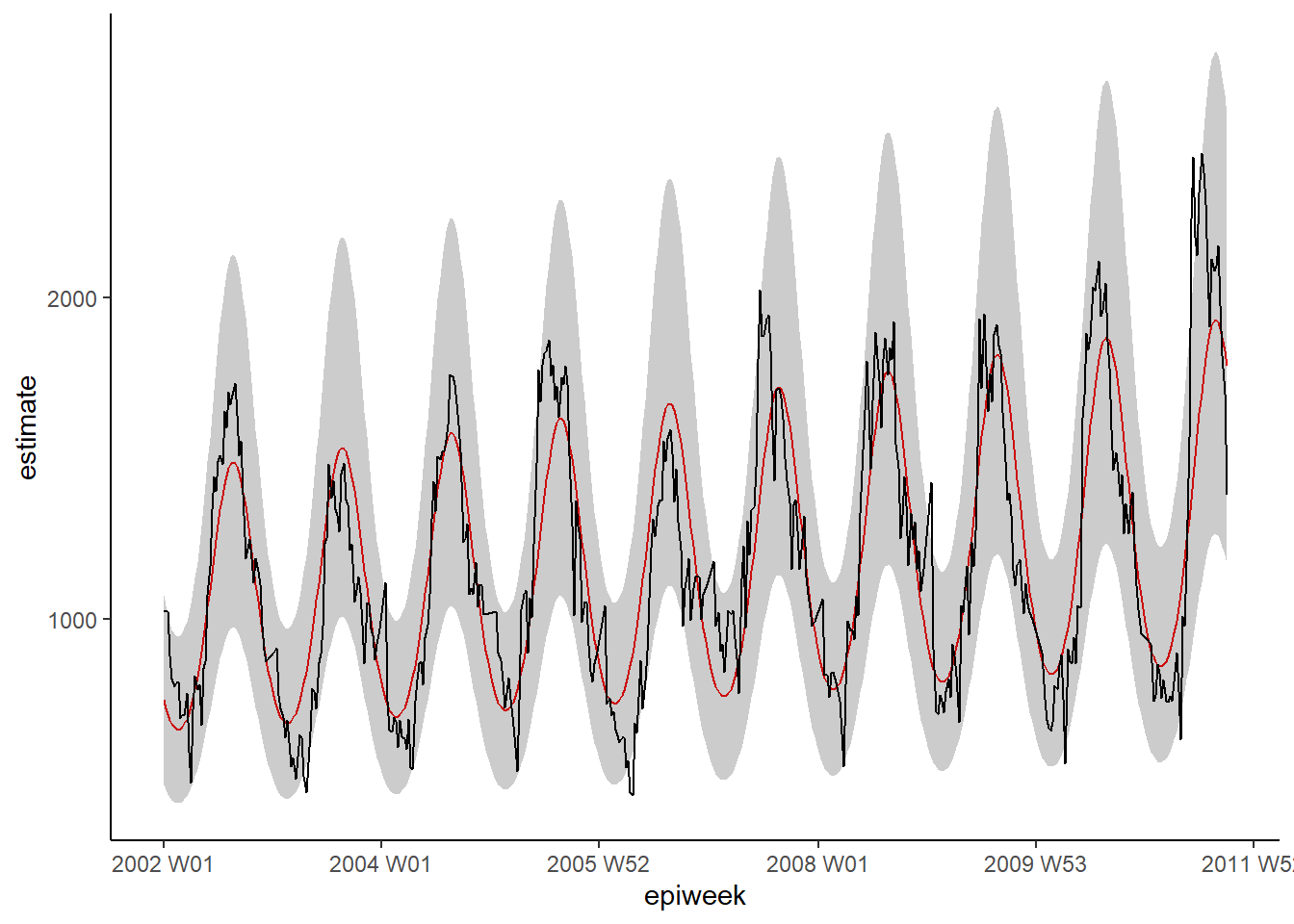
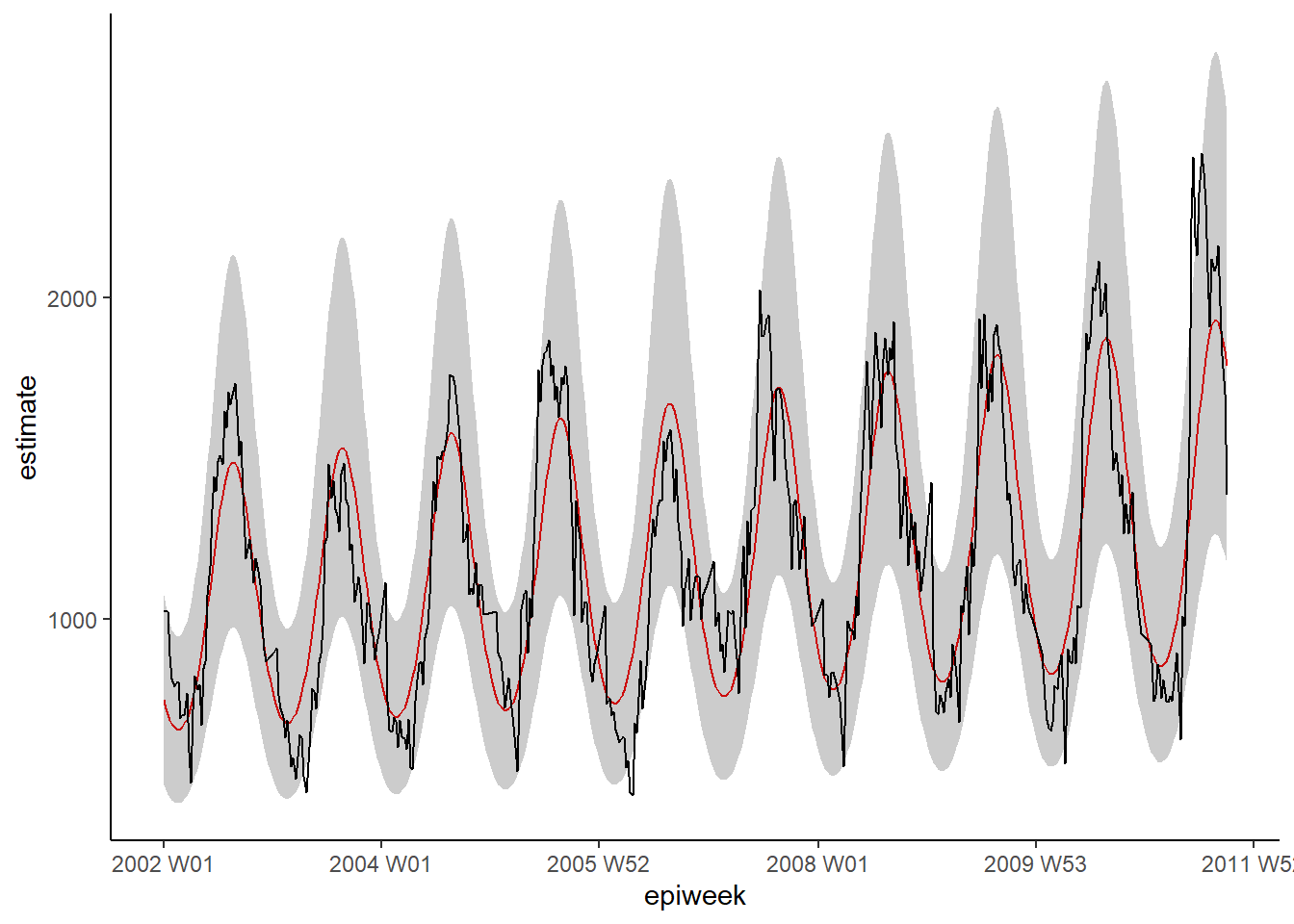
## representar la regresión
ggplot(data = estimate_res, aes(x = epiweek)) +
## añadir una línea para la estimación del modelo
geom_line(aes(y = estimate),
col = "Red") +
## añadir una banda para los intervalos de predicción
geom_ribbon(aes(ymin = lower_pi,
ymax = upper_pi),
alpha = 0.25) +
## añade una línea para los recuentos de casos observados
geom_line(aes(y = case_int),
col = "black") +
## crea un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic()Residuos
Para ver si nuestro modelo se ajusta a los datos observados, tenemos que observar los residuos. Los residuos son la diferencia entre los recuentos observados y los recuentos estimados a partir del modelo. Podríamos calcularlo simplemente utilizando case_int - estimate, pero la función residuals() lo extrae directamente de la regresión por nosotros.
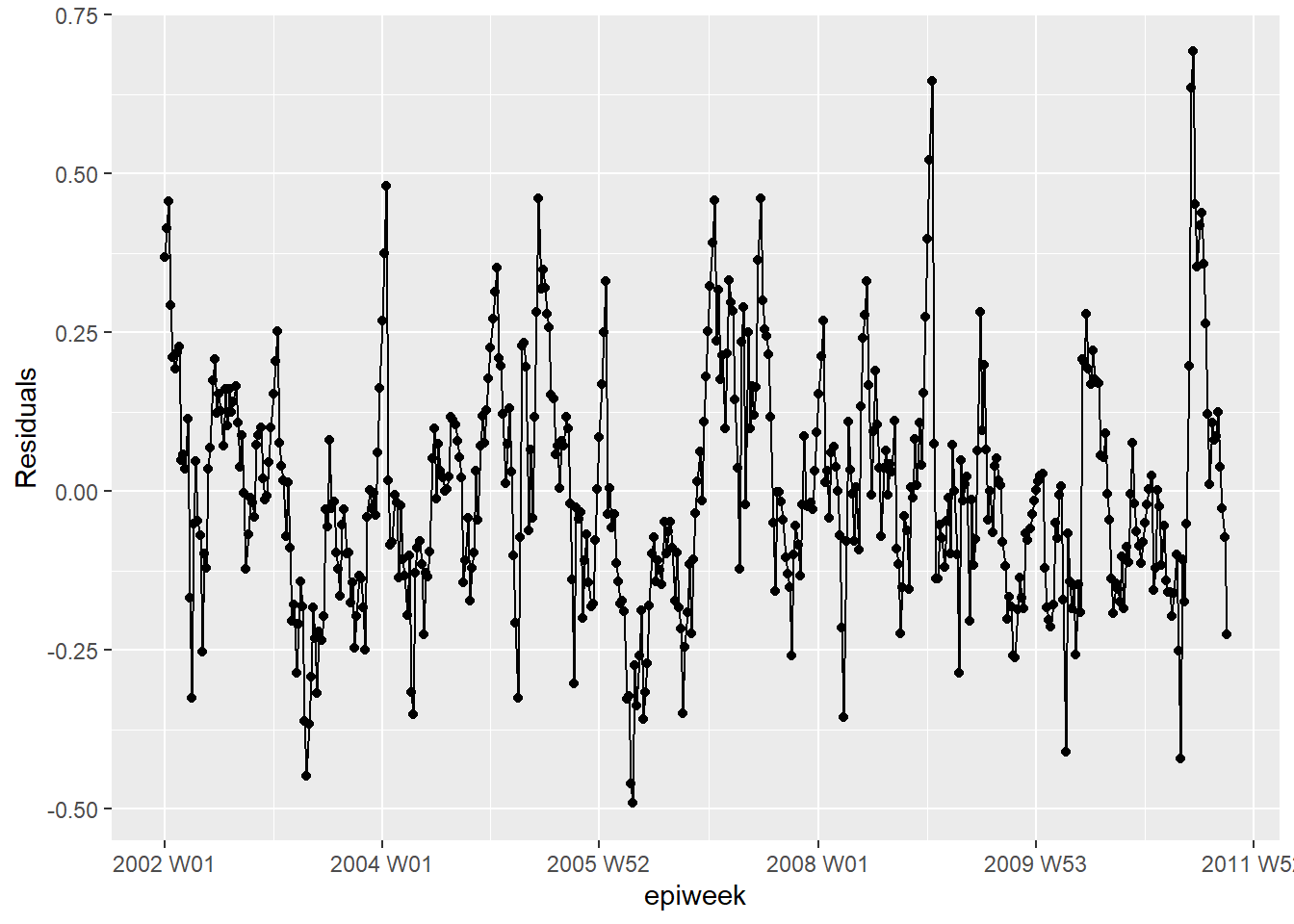
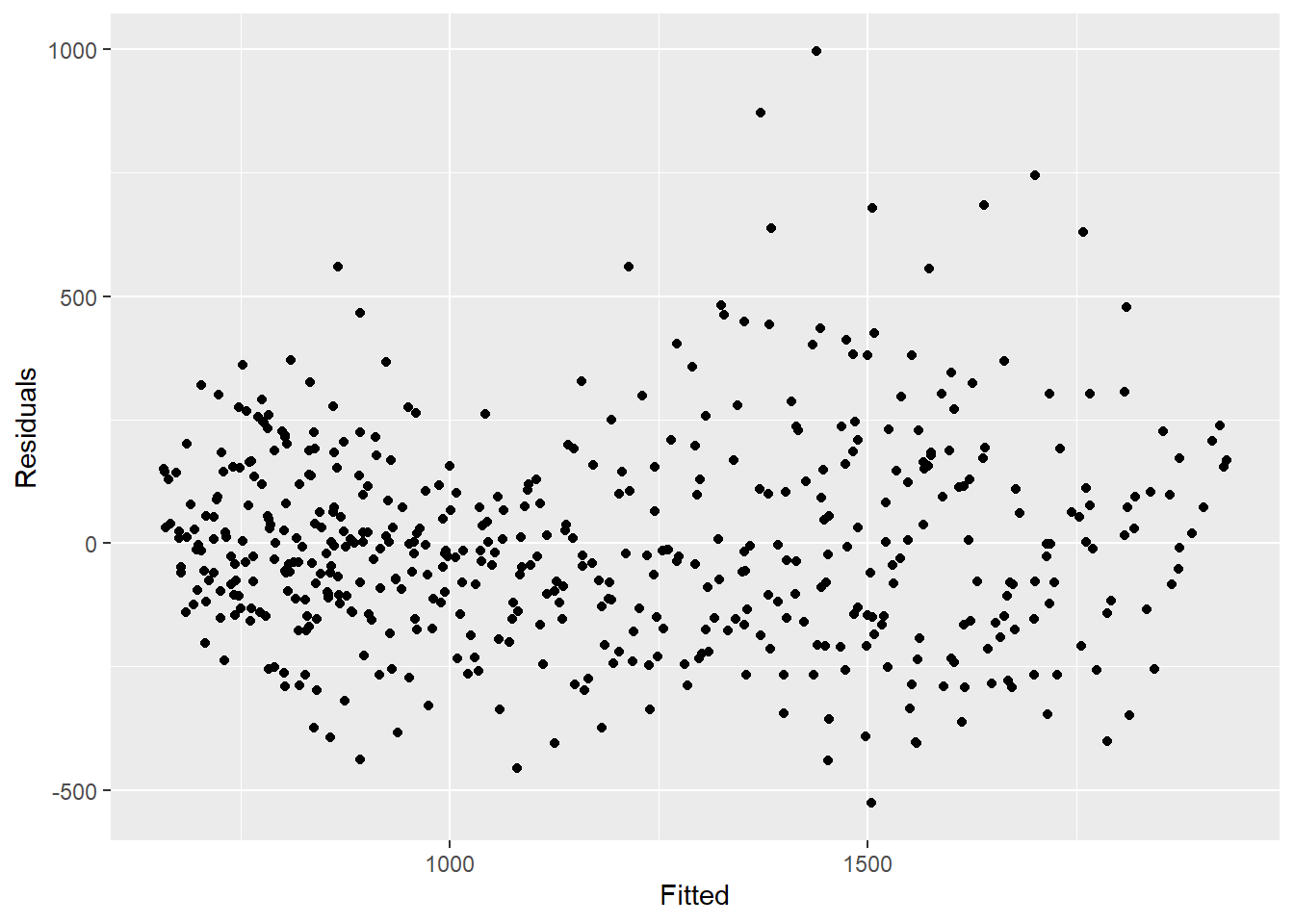
Lo que vemos a continuación es que no estamos explicando toda la variación que podríamos con el modelo. Es posible que debamos ajustar más términos de Fourier y abordar la amplitud. Sin embargo, para este ejemplo lo dejaremos como está. Los gráficos muestran que nuestro modelo es peor en los picos y en los valles (cuando los recuentos son los más altos y los más bajos) y que es más probable que subestime los recuentos observados.
## calcular los residuos
estimate_res <- estimate_res %>%
mutate(resid = fitted_model$result[[1]]$residuals)
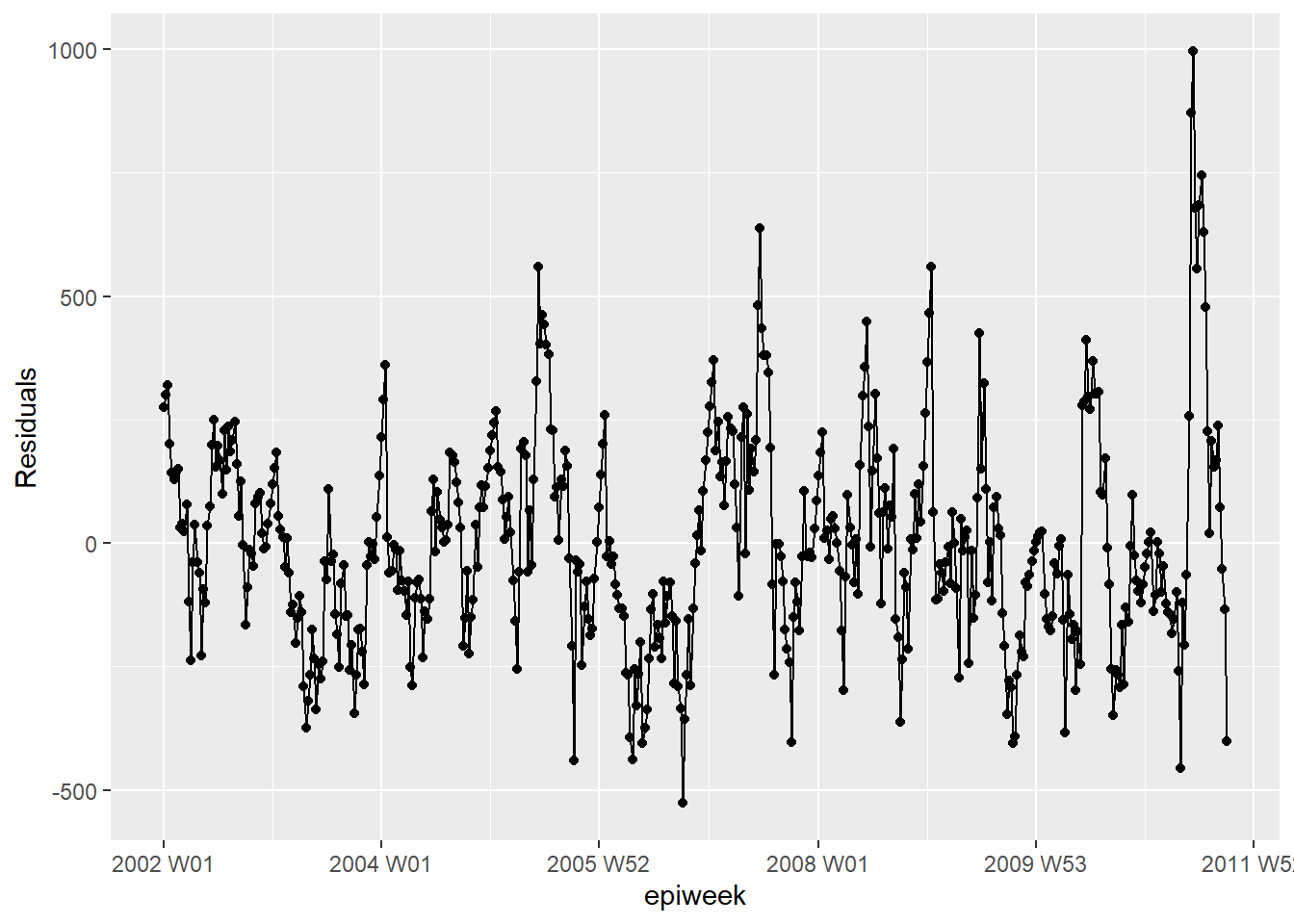
## ¿son los residuos bastante constantes a lo largo del tiempo (si no es así: brotes? ¿cambio en la práctica?)
estimate_res %>%
ggplot(aes(x = epiweek, y = resid)) +
geom_line() +
geom_point() +
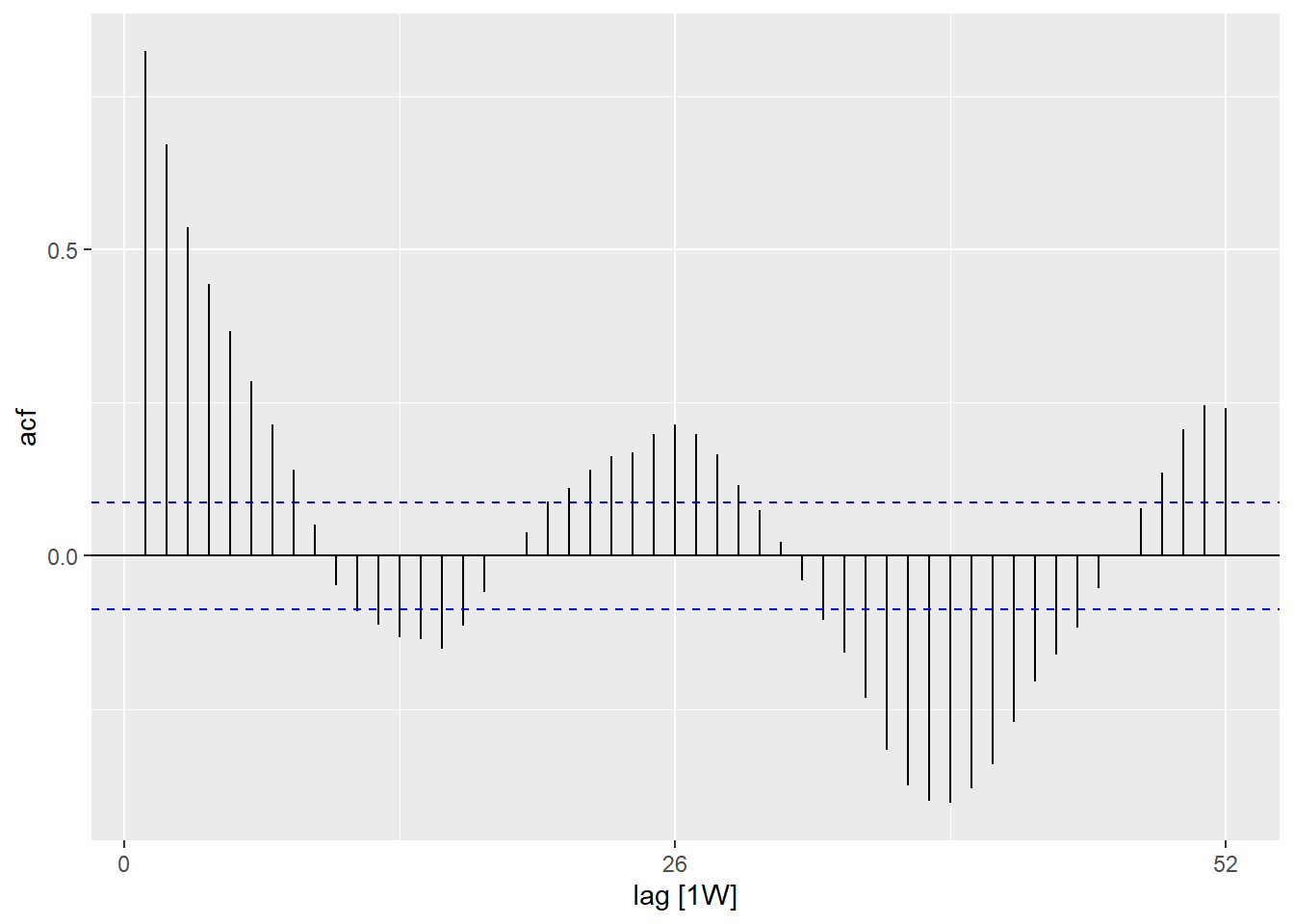
labs(x = "epiweek", y = "Residuals")## ¿hay autocorrelación en los residuos (hay un patrón en el error?)
estimate_res %>%
as_tsibble(index = epiweek) %>%
ACF(resid, lag_max = 52) %>%
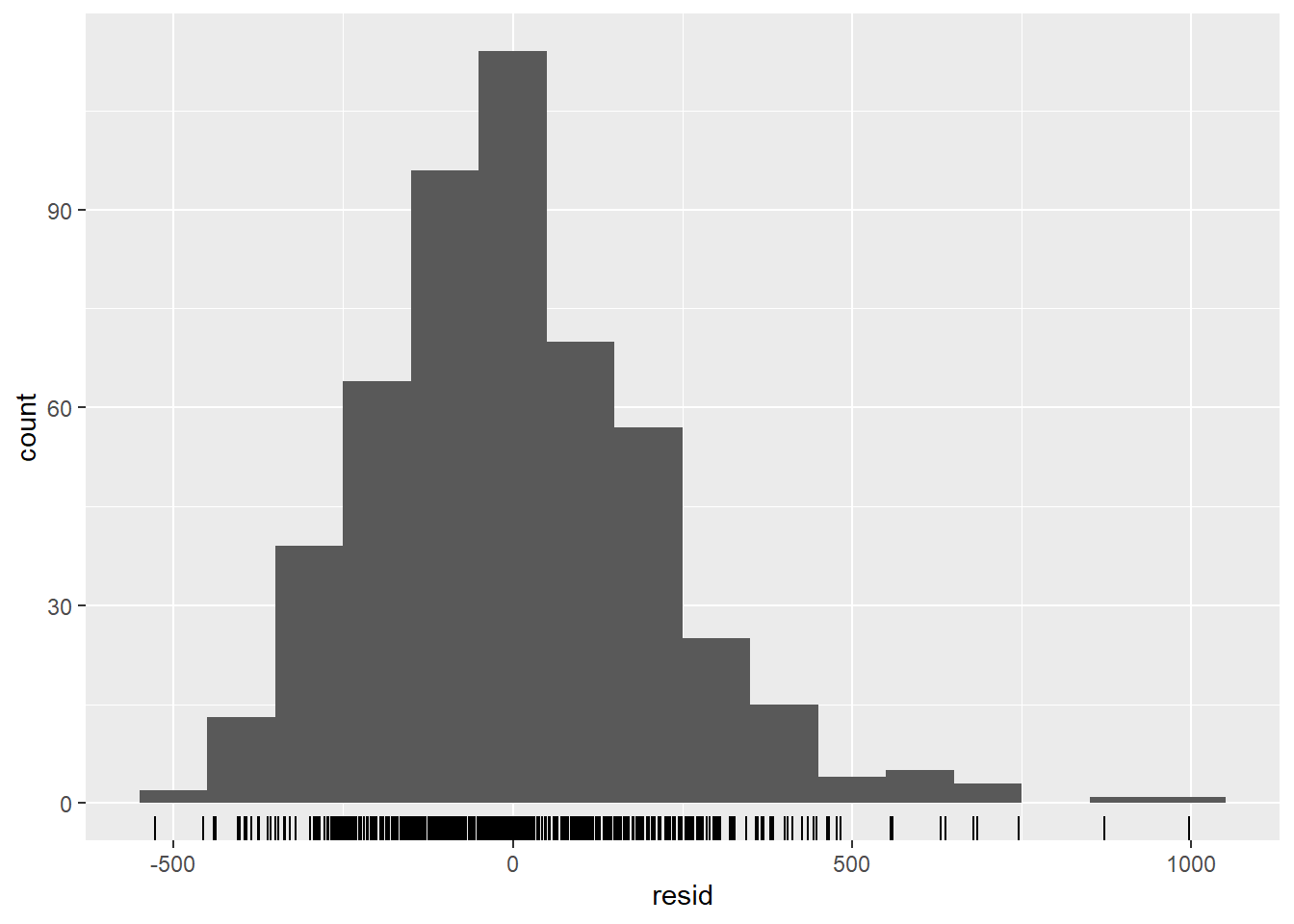
autoplot()## ¿se distribuyen normalmente los residuos (se subestiman o sobreestiman?)
estimate_res %>%
ggplot(aes(x = resid)) +
geom_histogram(binwidth = 100) +
geom_rug() +
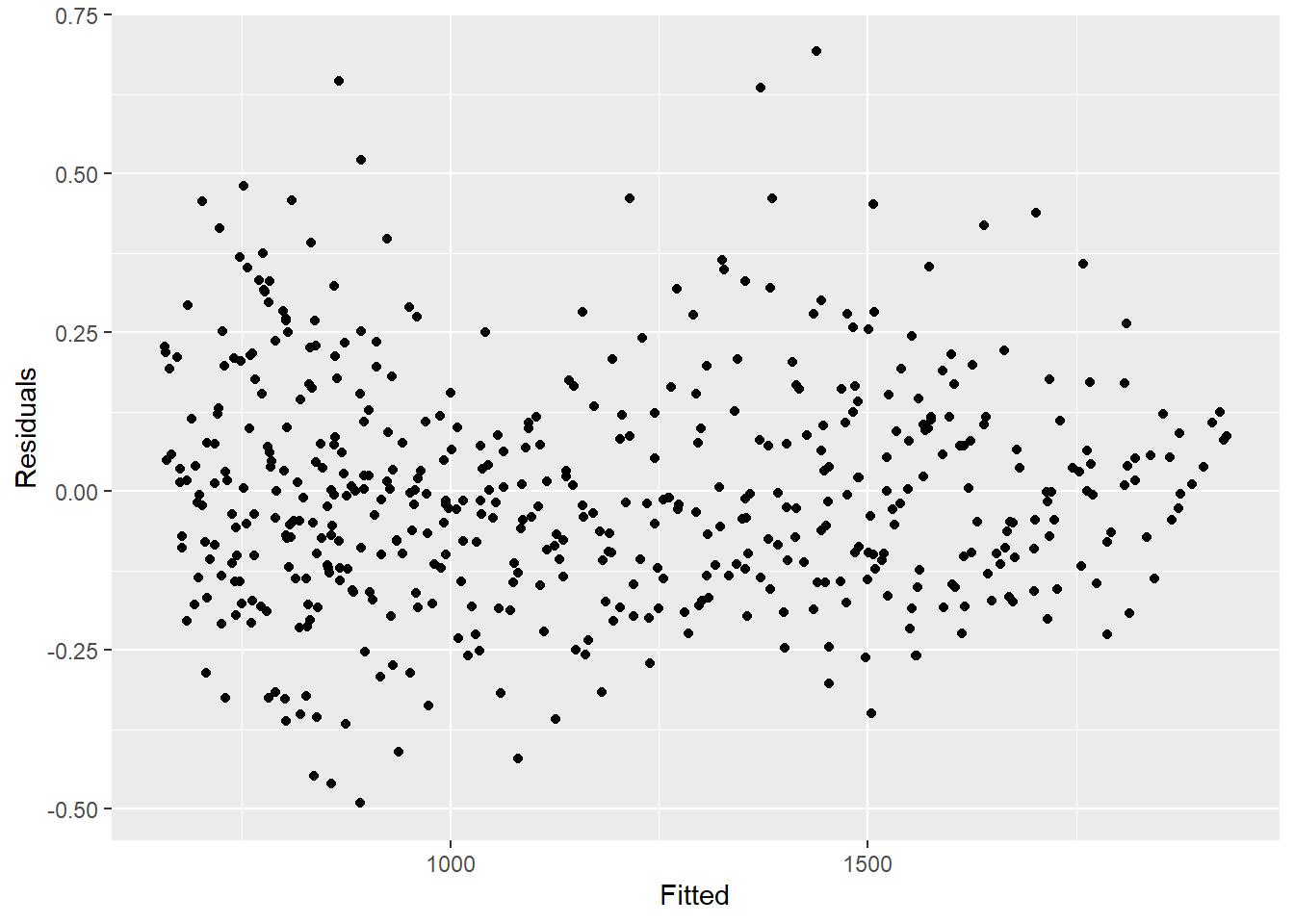
labs(y = "count") ## comparar los recuentos observados con sus residuos
## tampoco debería haber un patrón
estimate_res %>%
ggplot(aes(x = estimate, y = resid)) +
geom_point() +
labs(x = "Fitted", y = "Residuals")## probar formalmente la autocorrelación de los residuos
## H0 es que los residuos proceden de una serie de ruido blanco (es decir, aleatoria)
## prueba de independencia
## si el valor p es significativo entonces no es aleatorio
Box.test(estimate_res$resid, type = "Ljung-Box")
Box-Ljung test
data: estimate_res$resid
X-squared = 336.25, df = 1, p-value < 2.2e-1623.6 Relación de dos series temporales
En este caso, analizamos el uso de los datos meteorológicos (concretamente la temperatura) para explicar los recuentos de casos de campylobacter.
Fusión de conjuntos de datos
Podemos unir nuestros conjuntos de datos utilizando la variable semana (epiweek). Para obtener más información sobre la fusión, consulta la página del manual sobre unir datos
## left join para que sólo tengamos las filas ya existentes en counts
## elimina la variable fecha de temp_data (de lo contrario estará duplicada)
counts <- left_join(counts,
select(temp_data, -date),
by = "epiweek")Análisis descriptivo
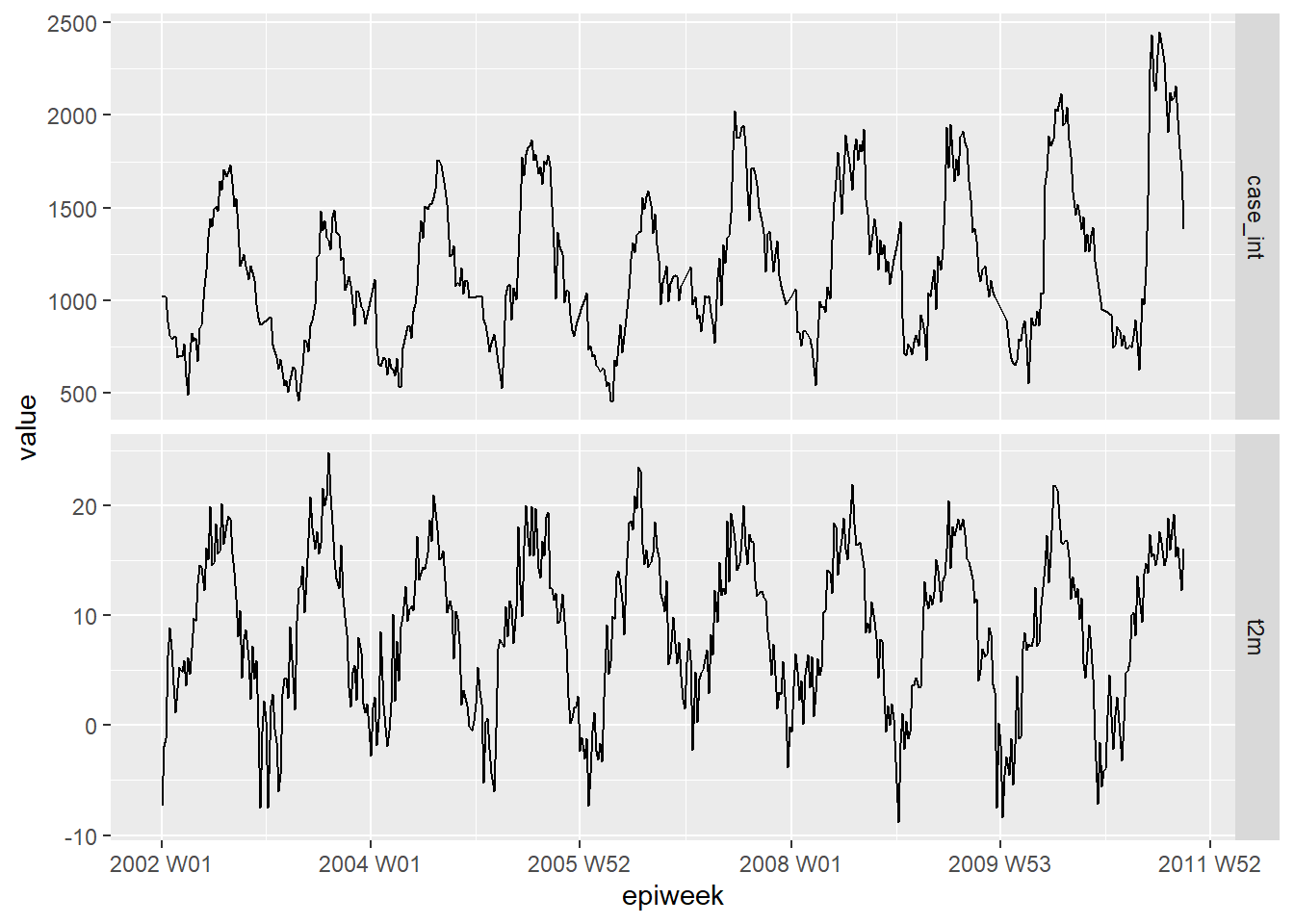
En primer lugar, traza los datos para ver si hay alguna relación evidente. El siguiente gráfico muestra que hay una clara relación en la estacionalidad de las dos variables, y que la temperatura puede alcanzar su punto máximo unas semanas antes que el número de casos. Para más información sobre pivotar datos, consulta la sección del manual sobre pivotar datos.
counts %>%
## conservar las variables que nos interesan
select(epiweek, case_int, t2m) %>%
## cambiar los datos a formato largo
pivot_longer(
## utiliza epiweek como la clave
!epiweek,
## mover los nombres de las columnas a la nueva columna "measure"
names_to = "measure",
## mover los valores de cell a la nueva columna " values"
values_to = "value") %>%
## crear un gráfico con el conjunto de datos anterior
## dibujar epiweek en el eje-x y valores (recuentos/celsius) en el eje-y
ggplot(aes(x = epiweek, y = value)) +
## crea un gráfico separado para los recuentos de temperaturas y casos
## dejar que establezcan sus propios ejes-y
facet_grid(measure ~ ., scales = "free_y") +
## dibuja ambos como una línea
geom_line()Retrasos y correlación cruzada
Para comprobar formalmente qué semanas están más relacionadas entre los casos y la temperatura. Podemos utilizar la función de correlación cruzada (CCF()) del paquete de feats. También se podría visualizar (en lugar de utilizar arrange) utilizando la función autoplot().
counts %>%
## calcular la correlación cruzada entre los recuentos interpolados y la temperatura
CCF(case_int, t2m,
## fija el desfase máximo en 52 semanas
lag_max = 52,
## devuelve el coeficiente de correlación
type = "correlation") %>%
## ordena el coeficiente de correlación en orden descendente
## muestra los retardos más asociados
arrange(-ccf) %>%
## muestra sólo los diez primeros
slice_head(n = 10)# A tsibble: 10 x 2 [1W]
lag ccf
<cf_lag> <dbl>
1 -4W 0.749
2 -5W 0.745
3 -3W 0.735
4 -6W 0.729
5 -2W 0.727
6 -7W 0.704
7 -1W 0.695
8 -8W 0.671
9 0W 0.649
10 47W 0.638Vemos que un desfase de 4 semanas es el más correlacionado, por lo que creamos una variable de temperatura retardada para incluirla en nuestra regresión.
PELIGRO: Ten en cuenta que las primeras cuatro semanas de nuestros datos en la variable de temperatura retardada faltan (NA) - ya que no hay cuatro semanas anteriores para obtener datos. Para utilizar este conjunto de datos con la función predict() de trending, necesitamos utilizar el argumento simulate_pi = FALSE dentro de predict() más abajo. Si quisiéramos utilizar la opción de simulación, entonces tenemos que eliminar estas pérdidas y almacenarlas como un nuevo conjunto de datos añadiendo drop_na(t2m_lag4) al fragmento de código que aparece a continuación.
counts <- counts %>%
## crea una nueva variable para la temperatura retardada cada cuatro semanas
mutate(t2m_lag4 = lag(t2m, n = 4))Binomial negativa con dos variables
Ajustamos una regresión binomial negativa como se hizo anteriormente. Esta vez añadimos la variable de temperatura con un retraso de cuatro semanas.
PRECAUCIóN: Observa el uso de simulate_pi = FALSE dentro del argumento predict(). Esto se debe a que el comportamiento por defecto de trending es utilizar el paquete ciTools para estimar un intervalo de predicción. Esto no funciona si hay recuentos NA, y también produce intervalos más granulares. Véase ?trending::predict.trending_model_fit para más detalles.
## define el modelo que se quiere ajustar (binomial negativo)
model <- glm_nb_model(
## establecer el número de casos como resultado de interés
case_int ~
## utiliza epiweek para tener en cuenta la tendencia
epiweek +
## usar los términos de fourier para tener en cuenta la estacionalidad
fourier +
### usa el retraso de cuatro semanas de la temperatura
t2m_lag4
)
## ajusta el modelo usando el conjunto de datos de recuentos
fitted_model <- trending::fit(model, data.frame(counts))
## calcula los intervalos de confianza y de predicción
observed <- predict(fitted_model, simulate_pi = FALSE)Para investigar los términos individuales, podemos sacar la regresión binomial negativa original del formato de trending utilizando get_model() y pasarla a la función tidy() del paquete broom para recuperar las estimaciones exponenciadas y los intervalos de confianza asociados.
Lo que esto nos muestra es que la temperatura retardada, tras controlar la tendencia y la estacionalidad, es similar a los recuentos de casos (estimación ~ 1) y está significativamente asociada. Esto sugiere que podría ser una buena variable para predecir el número de casos futuros (ya que las previsiones climáticas están disponibles).
fitted_model %>%
## extrae la regresión binomial negativa original
get_fitted_model() #%>% [[1]]
Call: glm.nb(formula = case_int ~ epiweek + fourier + t2m_lag4, data = data.frame(counts),
init.theta = 32.80689607, link = log)
Coefficients:
(Intercept) epiweek fourierS1-52 fourierC1-52 t2m_lag4
5.825e+00 8.464e-05 -2.850e-01 -1.954e-01 6.672e-03
Degrees of Freedom: 504 Total (i.e. Null); 500 Residual
(4 observations deleted due to missingness)
Null Deviance: 2015
Residual Deviance: 508.2 AIC: 6784 ## obtiene un dataframe ordenado de los resultados
# tidy(exponentiate = TRUE,
# conf.int = TRUE)Una rápida inspección visual del modelo muestra que se podría hacer un mejor trabajo de estimación de los recuentos de casos observados.
## traza la regresión
ggplot(data = estimate_res, aes(x = epiweek)) +
## añade una línea para la estimación del modelo
geom_line(aes(y = estimate),
col = "Red") +
## añade una banda para los intervalos de predicción
geom_ribbon(aes(ymin = lower_pi,
ymax = upper_pi),
alpha = 0.25) +
## añade una línea para los recuentos de casos observados
geom_line(aes(y = case_int),
col = "black") +
## crea un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic()Residuos
Volvemos a investigar los residuos para ver si nuestro modelo se ajusta a los datos observados. Los resultados y la interpretación aquí son similares a los de la regresión anterior, por lo que puede ser más factible quedarse con el modelo más simple sin temperatura.
## calcular los residuos
estimate_res <- estimate_res %>%
mutate(resid = case_int - estimate)
## ¿son los residuos bastante constantes a lo largo del tiempo (si no es así: brotes? ¿cambio en la práctica?)
estimate_res %>%
ggplot(aes(x = epiweek, y = resid)) +
geom_line() +
geom_point() +
labs(x = "epiweek", y = "Residuals")## ¿hay autocorrelación en los residuos (hay un patrón en el error?)
estimate_res %>%
as_tsibble(index = epiweek) %>%
ACF(resid, lag_max = 52) %>%
autoplot()## ¿se distribuyen normalmente los residuos (se subestiman o sobreestiman?)
estimate_res %>%
ggplot(aes(x = resid)) +
geom_histogram(binwidth = 100) +
geom_rug() +
labs(y = "count") ## compara los recuentos observados con sus residuales
## tampoco debería haber un patrón
estimate_res %>%
ggplot(aes(x = estimate, y = resid)) +
geom_point() +
labs(x = "Fitted", y = "Residuals")## probar formalmente la autocorrelación de los residuos
## H0 es que los residuos proceden de una serie de ruido blanco (es decir, aleatoria)
## prueba de independencia
## si el valor p es significativo entonces no es aleatorio
Box.test(estimate_res$resid, type = "Ljung-Box")
Box-Ljung test
data: estimate_res$resid
X-squared = 346.64, df = 1, p-value < 2.2e-1623.7 Detección de brotes
Aquí mostraremos dos métodos (similares) de detección de brotes. El primero se basa en las secciones anteriores. Utilizamos el paquete trending para ajustar las regresiones a los años anteriores, y luego predecir lo que esperamos ver en el año siguiente. Si los recuentos observados están por encima de lo que esperamos, esto podría sugerir que hay un brote. El segundo método se basa en principios similares, pero utiliza el paquete surveillance, que tiene varios algoritmos diferentes para la detección de aberraciones.
ATENCIÓN: Normalmente, estás interesado en el año actual (donde sólo se conocen los recuentos hasta la semana actual). Así que en este ejemplo pretendemos estar en la semana 39 de 2011.
Paquete trending
Para este método definimos una línea base (que normalmente debería ser de unos 5 años de datos). Ajustamos una regresión a los datos de referencia y la utilizamos para predecir las estimaciones del año siguiente.
Fecha de corte
Es más fácil definir las fechas en un lugar y luego utilizarlas en el resto del código.
Aquí definimos una fecha de inicio (cuando comenzaron nuestras observaciones) y una fecha de corte (el final de nuestro período de referencia - y cuando comienza el período que queremos predecir). ~También definimos cuántas semanas hay en nuestro año de interés (el que vamos a predecir)~. También definimos cuántas semanas hay entre nuestra fecha límite de referencia y la fecha final para la que nos interesa predecir.
NOTA: En este ejemplo pretendemos estar actualmente a finales de septiembre de 2011 (“2011 W39”).
## define la fecha de inicio (cuando empezaron las observaciones)
start_date <- min(counts$epiweek)
## define una semana de corte (fin de la línea base, inicio del periodo de predicción)
cut_off <- yearweek("2010-12-31")
## define la última fecha de interés (es decir, el final de la predicción)
end_date <- yearweek("2011-12-31")
## encontrar cuántas semanas en el período (año) de interés
num_weeks <- as.numeric(end_date - cut_off)Añadir filas
Para poder pronosticar en un formato tidyverse, necesitamos tener el número correcto de filas en nuestro conjunto de datos, es decir, una fila por cada semana hasta la end_date (fecha de corte) definida anteriormente. El código siguiente permite añadir estas filas por una variable de agrupación - por ejemplo, si tuviéramos varios países en unos datos, podríamos agrupar por país y luego añadir filas apropiadas para cada uno. La función group_by_key() de tsibble nos permite hacer esta agrupación y luego pasar los datos agrupados a las funciones de dplyr, group_modify() y add_row(). Luego especificamos la secuencia de semanas entre una después de la semana máxima disponible actualmente en los datos y la semana final.
## añade las semanas que faltan hasta final de año
counts <- counts %>%
## agrupa por región
group_by_key() %>%
## para cada grupo, añade filas desde la mayor epiweek hasta el final del año
group_modify(~add_row(.,
epiweek = seq(max(.$epiweek) + 1,
end_date,
by = 1)))Términos de Fourier
Tenemos que redefinir nuestros términos de fourier, ya que queremos ajustarlos sólo a la fecha de referencia y luego predecir (extrapolar) esos términos para el año siguiente. Para ello tenemos que combinar dos listas de salida de la función fourier() juntas; la primera es para los datos de referencia, y la segunda predice para el año de interés (definiendo el argumento h).
N.b. para enlazar filas tenemos que usar rbind() (en lugar de bind_rows de tidyverse) ya que las columnas de fourier son una lista (por lo que no se nombran individualmente).
## define los términos de fourier (sencos)
counts <- counts %>%
mutate(
## combina los términos de fourier para las semanas anteriores y posteriores a la fecha límite de 2010
## (nb. los términos de fourier de 2011 están proyectados)
fourier = rbind(
## obtiene los términos de fourier de años anteriores
fourier(
## conserva sólo las filas anteriores a 2011
filter(counts,
epiweek <= cut_off),
## incluye un conjunto de términos sen cos
K = 1
),
## predice los términos de fourier para 2011 (usando datos de referencia)
fourier(
## conserva sólo las filas anteriores a 2011
filter(counts,
epiweek <= cut_off),
## incluye un conjunto de términos sen cos
K = 1,
## predice con 52 semanas de antelación
h = num_weeks
)
)
)Dividir los datos y ajustar la regresión
Ahora tenemos que dividir nuestro conjunto de datos en el período de referencia y el período de predicción. Esto se hace utilizando la función group_split() de dplyr después de group_by(), y creará una lista con dos dataframes, uno para antes de tu corte y otro para después.
A continuación, utilizamos la función pluck() del paquete purrr para extraer los datos del listado (lo que equivale a utilizar corchetes, por ejemplo, dat[1]]), y podemos ajustar nuestro modelo a los datos de referencia, y luego utilizar la función predict() para nuestros datos de interés después del corte.
Consulta la página sobre Iteración, bucles y listas para saber más sobre purrr.
ATENCIÓN: Observa el uso de simulate_pi = FALSE dentro del argumento predict(). Esto se debe a que el comportamiento por defecto de trending es utilizar el paquete ciTools para estimar un intervalo de predicción. Esto no funciona si hay recuentos NA, y también produce intervalos más granulares. Véase ?trending::predict.trending_model_fit para más detalles.
# divide los datos para el ajuste y la predicción
dat <- counts %>%
group_by(epiweek <= cut_off) %>%
group_split()
## define el modelo que se desea ajustar (binomial negativa)
model <- glm_nb_model(
## establece el número de casos como resultado de interés
case_int ~
## usa epiweek para tener en cuenta la tendencia
epiweek +
## utiliza los términos furier para tener en cuenta la estacionalidad
fourier
)
# define qué datos utilizar para el ajuste y cuáles para la predicción
fitting_data <- pluck(dat, 2)
pred_data <- pluck(dat, 1) %>%
select(case_int, epiweek, fourier)
# ajusta el modelo
fitted_model <- trending::fit(model, data.frame(fitting_data))
# obtiene intervalos de confianza y estimaciones para los datos ajustados
observed <- fitted_model %>%
predict(simulate_pi = FALSE)
# pronostica con los datos con los que se quiere predecir
forecasts <- fitted_model %>%
predict(data.frame(pred_data), simulate_pi = FALSE)
## combina los conjuntos de datos de referencia y de predicción
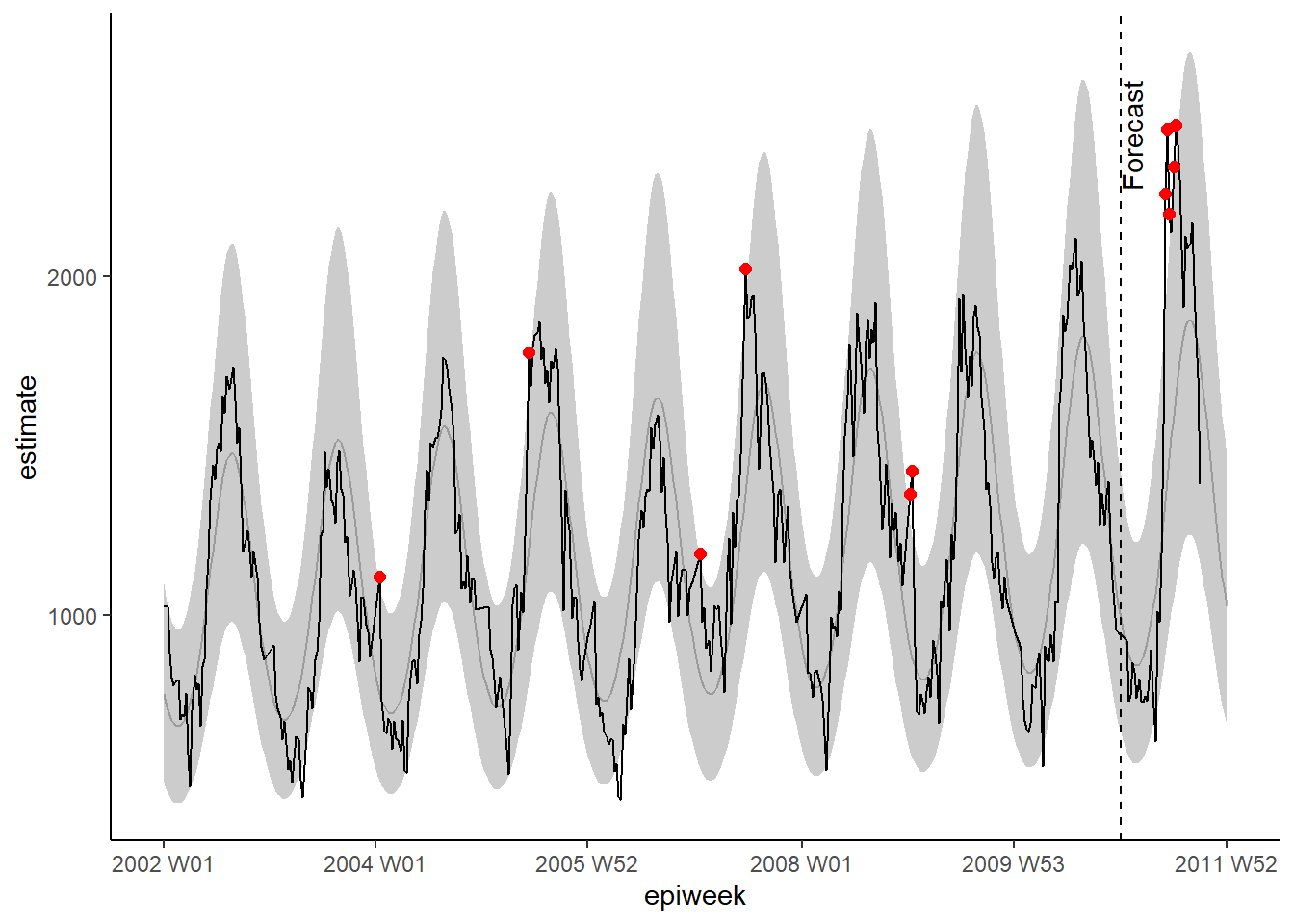
observed <- bind_rows(observed$result, forecasts$result)Como anteriormente, podemos visualizar nuestro modelo con ggplot. Resaltamos las alertas con puntos rojos para los recuentos observados por encima del intervalo de predicción del 95%. Esta vez también añadimos una línea vertical para etiquetar cuándo empieza la predicción. ##hastaqui
## representar la regresión
ggplot(data = observed, aes(x = epiweek)) +
## añade una línea para la estimación del modelo
geom_line(aes(y = estimate),
col = "grey") +
## añade una banda para los intervalos de predicción
geom_ribbon(aes(ymin = lower_pi,
ymax = upper_pi),
alpha = 0.25) +
## añade una línea para los recuentos de casos observados
geom_line(aes(y = case_int),
col = "black") +
## representar en puntos los recuentos observados por encima de lo esperado
geom_point(
data = filter(observed, case_int > upper_pi),
aes(y = case_int),
colour = "red",
size = 2) +
## añade una línea vertical y una etiqueta para mostrar dónde empieza la previsión
geom_vline(
xintercept = as.Date(cut_off),
linetype = "dashed") +
annotate(geom = "text",
label = "Forecast",
x = cut_off,
y = max(observed$upper_pi) - 250,
angle = 90,
vjust = 1
) +
## realiza un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic()Warning: Removed 13 rows containing missing values or values outside the scale range
(`geom_line()`).Validación de la predicción
Más allá de la inspección de los residuos, es importante investigar lo bueno que es tu modelo para predecir casos en el futuro. Esto te da una idea de la fiabilidad de tus umbrales de alerta.
La forma tradicional de validar es ver lo bien que se puede predecir el último año anterior al actual (porque aún no se conocen los recuentos del “año actual”). Por ejemplo, en nuestro conjunto de datos, utilizaríamos los datos de 2002 a 2009 para predecir 2010, y luego veríamos la precisión de esas predicciones. A continuación, volveríamos a ajustar el modelo para incluir los datos de 2010 y los utilizaríamos para predecir los recuentos de 2011.
Como puede verse en la siguiente figura de Hyndman et al en “Forecasting principles and practice”.
 figura reproducida con permiso de los autores
figura reproducida con permiso de los autores
La desventaja de esto es que no estás usando todos los datos disponibles, y no es el modelo final que estás usando para la predicción.
Una alternativa es utilizar un método llamado validación cruzada. En este caso, se pasan todos los datos disponibles para ajustar múltiples modelos de predicción a un año vista. Se utilizan cada vez más datos en cada modelo, como se ve en la siguiente figura del mismo [texto de Hyndman et al]((https://otexts.com/fpp3/). Por ejemplo, el primer modelo utiliza 2002 para predecir 2003, el segundo utiliza 2002 y 2003 para predecir 2004, y así sucesivamente.  figura reproducida con permiso de los autores
figura reproducida con permiso de los autores
A continuación, utilizamos la función map() del paquete purrr para recorrer cada conjunto de datos. Luego, ponemos las estimaciones conjunto de datos y las fusionamos con los recuentos de casos originales, para utilizar el paquete yardstick para calcular las medidas de precisión. Calculamos cuatro medidas que incluyen: Error medio cuadrático (RMSE), Error medio absoluto (MAE), Error medio absoluto a escala (MASE), Error medio porcentual absoluto (MAPE).
ATENCIÓN: Observa el uso de simulate_pi = FALSE dentro del argumento predict(). Esto se debe a que el comportamiento por defecto de la tendencia es utilizar el paquete ciTools para estimar un intervalo de predicción. Esto no funciona si hay recuentos NA, y también produce intervalos más granulares. Véase ?trending::predict.trending_model_fit para más detalles.
## Validación cruzada: predicción de la(s) semana(s) anterior(es) basada en una ventana deslizante.
## amplía los datos en ventanas de 52 semanas (antes + después)
## para predecir 52 semanas por delante
## (crea cadenas de observaciones cada vez más largas - mantiene los datos más antiguos)
## define la ventana que se quiere utilizar
roll_window <- 52
## define las semanas que se quieren predecir
weeks_ahead <- 52
## crea un conjunto de datos repetidos, cada vez más largos
## etiqueta cada conjunto de datos con un id único
## utiliza sólo casos anteriores al año de interés (es decir, 2011)
case_roll <- counts %>%
filter(epiweek < cut_off) %>%
## mantiene sólo las variables de semana y recuento de casos
select(epiweek, case_int) %>%
## elimina las últimas x observaciones
## dependiendo de cuántas semanas se prevean
## (de lo contrario será una previsión real a "desconocido")
slice(1:(n() - weeks_ahead)) %>%
as_tsibble(index = epiweek) %>%
## desplaza cada semana en x después de las ventanas para crear ID de agrupación
## dependiendo de lo que especifique roll_window
stretch_tsibble(.init = roll_window, .step = 1) %>%
## elimina el primer par - ya que no tiene casos "anteriores"
filter(.id > roll_window)
## para cada uno de los grupos de datos únicos se ejecuta el código siguiente
forecasts <- purrr::map(unique(case_roll$.id),
function(i) {
## sólo se mantiene el conjunto actual que se está ajustando
mini_data <- filter(case_roll, .id == i) %>%
as_tibble()
## crea un conjunto de datos vacío para la previsión
forecast_data <- tibble(
epiweek = seq(max(mini_data$epiweek) + 1,
max(mini_data$epiweek) + weeks_ahead,
by = 1),
case_int = rep.int(NA, weeks_ahead),
.id = rep.int(i, weeks_ahead)
)
# añade los datos de previsión a los originales
mini_data <- bind_rows(mini_data, forecast_data)
## define los puntos de corte en función de los últimos datos de recuento no faltantes
cv_cut_off <- mini_data %>%
## conserva sólo las filas no faltantes
drop_na(case_int) %>%
## obtiene la última semana
summarise(max(epiweek)) %>%
## extrae lo que no está en un dataframe
pull()
## convierte mini_data en un tsibble
mini_data <- tsibble(mini_data, index = epiweek)
## define los términos de fourier (sencos)
mini_data <- mini_data %>%
mutate(
## combina los términos de fourier para las semanas anteriores y posteriores a la fecha de corte
fourier = rbind(
## obtiene los términos de fourier de años anteriores
forecast::fourier(
## conserva sólo las filas anteriores a la fecha de corte
filter(mini_data,
epiweek <= cv_cut_off),
## incluye un conjunto de términos sen cos
K = 1
),
## predice los términos de fourier para el año siguiente (utilizando los datos de referencia)
fourier(
## conserva sólo las filas anteriores al corte
filter(mini_data,
epiweek <= cv_cut_off),
## incluye un conjunto de términos seno-cos
K = 1,
## predice con 52 semanas de antelación
h = weeks_ahead
)
)
)
# divide los datos para el ajuste y la predicción
dat <- mini_data %>%
group_by(epiweek <= cv_cut_off) %>%
group_split()
## define el modelo que se quiere ajustar (binomial negativa)
model <- glm_nb_model(
## establece el número de casos como resultado de interés
case_int ~
## utiliza epiweek para tener en cuenta la tendencia
epiweek +
## usa los términos de furier para tener en cuenta la estacionalidad
fourier
)
# define qué datos utilizar para el ajuste y cuáles para la predicción
fitting_data <- pluck(dat, 2)
pred_data <- pluck(dat, 1)
# ajusta el modelo
fitted_model <- trending::fit(model, fitting_data)
# proyecta con los datos que se quieren predecir
forecasts <- fitted_model %>%
predict(data.frame(pred_data), simulate_pi = FALSE)
forecasts <- data.frame(forecasts$result[[1]]) %>%
## conserva sólo la semana y la estimación de la previsión
select(epiweek, estimate)
}
)
## convierte la lista en un dataframe con todas las proyecciones
forecasts <- bind_rows(forecasts)
## une las proyecciones con los datos observados
forecasts <- left_join(forecasts,
select(counts, epiweek, case_int),
by = "epiweek")
## usando {yardstick} calcula las métricas
## RMSE: Root mean squared error (error cuadrático medio)
## MAE: Error medio absoluto
## MASE: Mean absolute scaled error (Error medio absoluto a escala)
## MAPE: Error porcentual medio absoluto
model_metrics <- bind_rows(
## compara lo observado con lo proyectado en el conjunto de datos de previsiones
rmse(forecasts, case_int, estimate),
mae( forecasts, case_int, estimate),
mase(forecasts, case_int, estimate),
mape(forecasts, case_int, estimate),
) %>%
## conserva sólo el tipo de métrica y su salida
select(Metric = .metric,
Measure = .estimate) %>%
## convierte en formato ancho para poder enlazar filas después
pivot_wider(names_from = Metric, values_from = Measure)
## devuelve las métricas del modelo
model_metrics# A tibble: 1 × 4
rmse mae mase mape
<dbl> <dbl> <dbl> <dbl>
1 252. 199. 1.96 17.3paquete surveillance
En esta sección utilizamos el paquete surveillance para crear umbrales de alerta basados en algoritmos de detección de brotes. Hay varios métodos diferentes disponibles en el paquete, aunque aquí nos centraremos en dos opciones. Para más detalles, consulta estos documentos sobre la aplicación y la teoría de los algoritmos utilizados.
La primera opción utiliza el método Farrington mejorado. Este método ajusta un glm binomial negativo (incluyendo la tendencia) y pondera a la baja los brotes pasados (valores atípicos) para crear un nivel de umbral.
La segunda opción utiliza el método glrnb. Esto también se ajusta a un glm binomial negativo, pero incluye la tendencia y los términos de fourier (por lo que se favorece aquí). La regresión se utiliza para calcular la “media de control” (~valores ajustados), y a continuación se utiliza un estadístico de relación de verosimilitud generalizada para evaluar si hay un cambio en la media de cada semana. Ten en cuenta que el umbral de cada semana tiene en cuenta las semanas anteriores, por lo que si hay un cambio sostenido se activará una alarma. (También hay que tener en cuenta que después de cada alarma el algoritmo se reinicia)
Para trabajar con el paquete surveillance, primero tenemos que definir un objeto “surveillance time series” (utilizando la función sts()) para que encaje en el marco de trabajo.
## define el objeto series temporales de vigilancia
## nota. se puede incluir un denominador con el objeto población (ver ?sts)
counts_sts <- sts(observed = counts$case_int[!is.na(counts$case_int)],
start = c(
## subconjunto para mantener sólo el año desde start_date
as.numeric(str_sub(start_date, 1, 4)),
## subconjunto para mantener sólo la semana a partir de start_date
as.numeric(str_sub(start_date, 7, 8))),
## define el tipo de datos (en este caso semanales)
freq = 52)
## define el rango de semanas que se quiere incluir (es decir, el periodo de predicción)
## nota: el objeto sts sólo cuenta las observaciones sin asignarles un identificador de semana o año.
## identificador de año - utilizaremos nuestros datos para definir las observaciones adecuadas
weekrange <- cut_off - start_dateMétodo Farrington
A continuación, definimos cada uno de nuestros parámetros para el método Farrington en una list. A continuación, ejecutamos el algoritmo utilizando farringtonFlexible() y luego podemos extraer el umbral de una alerta utilizando farringtonmethod@upperbound para incluirlo en nuestro conjunto de datos. También es posible extraer un TRUE/FALSE para cada semana si se activó una alerta (estaba por encima del umbral) utilizando farringtonmethod@alarm.
## define control
ctrl <- list(
## define para qué periodo de tiempo se quiere el umbral (por ejemplo, 2011)
range = which(counts_sts@epoch > weekrange),
b = 9, ## cuántos años hacia atrás para la línea base
w = 2, ## tamaño de la ventana móvil en semanas
weightsThreshold = 2.58, ## reponderar brotes pasados (método noufaily mejorado - original sugiere 1)
## pastWeeksNotIncluded = 3, ## utiliza todas las semanas disponibles (noufaily sugiere dejar 26)
trend = TRUE,
pThresholdTrend = 1, ## 0.05 normalmente, sin embargo se aconseja 1 en el método mejorado (es decir, mantener siempre)
thresholdMethod = "nbPlugin",
populationOffset = TRUE
)
## aplicar el método farrington flexible
farringtonmethod <- farringtonFlexible(counts_sts, ctrl)
## crea una nueva variable en el conjunto de datos original llamada umbral
## que contiene el límite superior de farrington
## nota: esto es solo para las semanas de 2011 (por lo que hay que hacer un subconjunto de filas)
counts[which(counts$epiweek >= cut_off &
!is.na(counts$case_int)),
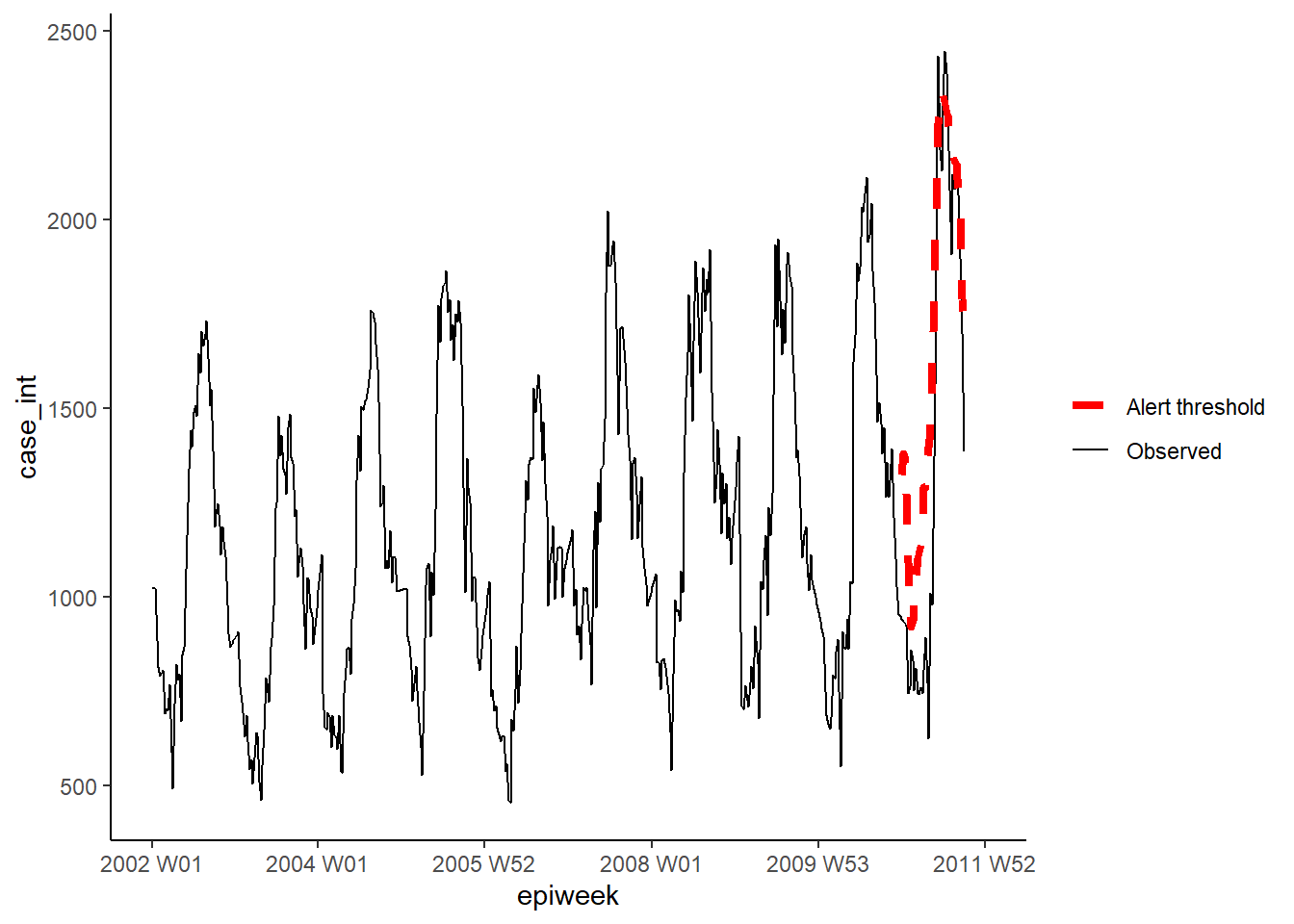
"threshold"] <- farringtonmethod@upperboundA continuación, podemos visualizar los resultados en ggplot como se hizo anteriormente.
ggplot(counts, aes(x = epiweek)) +
## añade los recuentos de casos observados como una línea
geom_line(aes(y = case_int, colour = "Observed")) +
## añade el límite superior del algoritmo de aberración
geom_line(aes(y = threshold, colour = "Alert threshold"),
linetype = "dashed",
size = 1.5) +
## define los colores
scale_colour_manual(values = c("Observed" = "black",
"Alert threshold" = "red")) +
## realiza un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic() +
## elimina el título de la leyenda
theme(legend.title = element_blank())Método GLRNB
Del mismo modo, para el método GLRNB definimos cada uno de nuestros parámetros en una list, luego ajustamos el algoritmo y extraemos los límites superiores.
ATENCIÓN: Este método utiliza la “fuerza bruta” (similar al bootstrapping) para calcular los umbrales, por lo que puede llevar mucho tiempo.
Consulta la viñeta GLRNB para más detalles.
## define las opciones de control
ctrl <- list(
## define para qué periodo de tiempo se quiere el umbral (por ejemplo, 2011)
range = which(counts_sts@epoch > weekrange),
mu0 = list(S = 1, ## número de términos de fourier (armónicos) a incluir
trend = TRUE, ## si incluye la tendencia o no
refit = FALSE), ## si se reajusta el modelo después de cada alarma
## cARL = umbral para el estadístico GLR (arbitrario)
## 3 ~ término medio para minimizar los falsos positivos
## 1 se ajusta al 99%PI de glm.nb - con cambios después de los picos (umbral reducido para la alerta)
c.ARL = 2,
# theta = log(1.5), ## equivale a un aumento del 50% de casos en un brote
ret = "cases" ## devuelve el límite superior del umbral como recuento de casos
)
## aplica el método glrnb
glrnbmethod <- glrnb(counts_sts, control = ctrl, verbose = FALSE)
## crea una nueva variable en el conjunto de datos original llamada umbral
## que contiene el límite superior de glrnb
## nota: esto es solo para las semanas de 2011 (por lo que hay que hacer un subconjunto de filas)
counts[which(counts$epiweek >= cut_off &
!is.na(counts$case_int)),
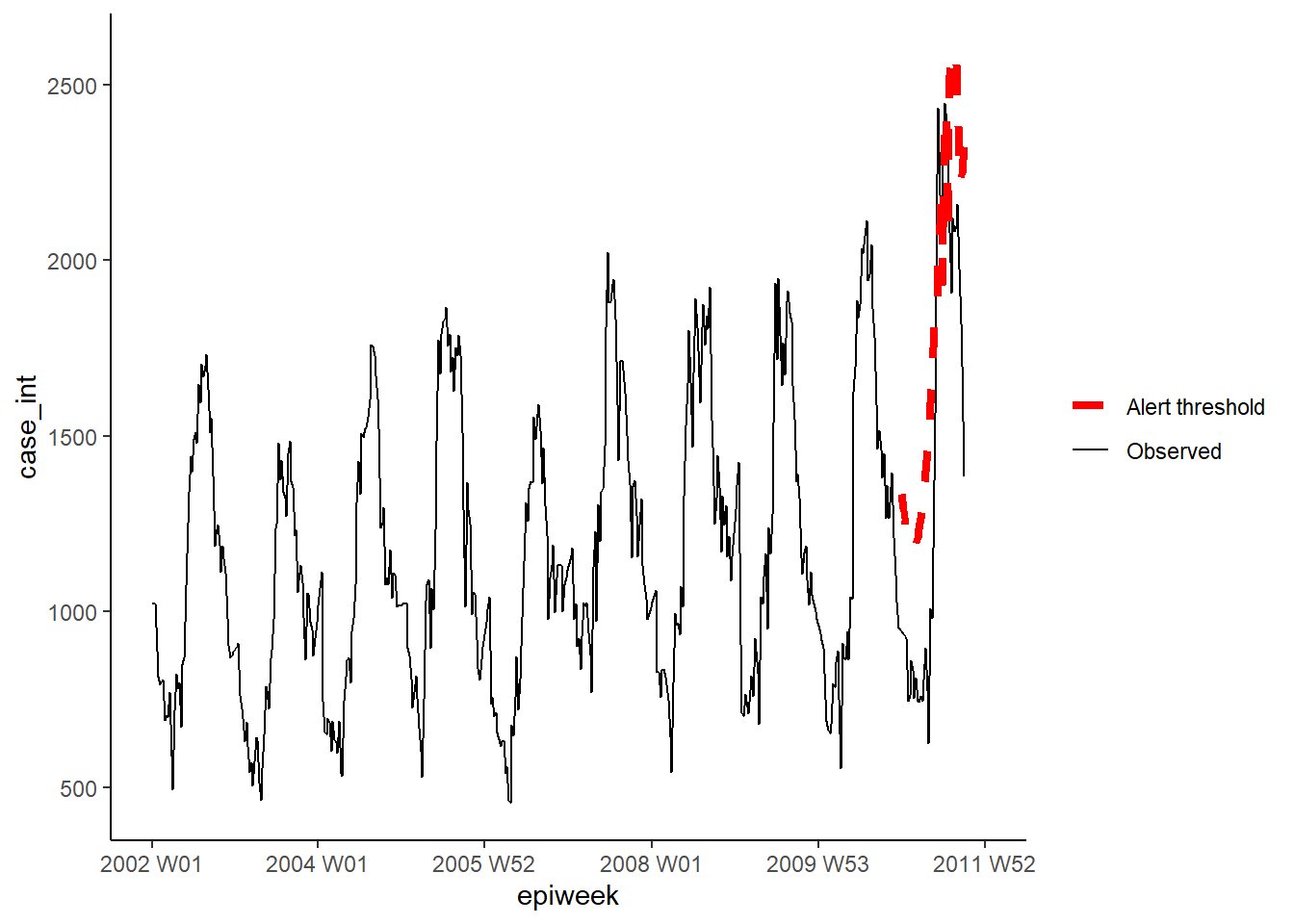
"threshold_glrnb"] <- glrnbmethod@upperboundVisualiza los resultados como antes.
ggplot(counts, aes(x = epiweek)) +
## añade los recuentos de casos observados como una línea
geom_line(aes(y = case_int, colour = "Observed")) +
## añade el límite superior del algoritmo de aberración
geom_line(aes(y = threshold_glrnb, colour = "Alert threshold"),
linetype = "dashed",
size = 1.5) +
## define los colores
scale_colour_manual(values = c("Observed" = "black",
"Alert threshold" = "red")) +
## realiza un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic() +
## elimina el título de la leyenda
theme(legend.title = element_blank())23.8 Series temporales interrumpidas
Las series temporales interrumpidas (también llamadas análisis de regresión segmentada o de intervención), se utilizan a menudo para evaluar el impacto de las vacunas en la incidencia de la enfermedad. Pero puede utilizarse para evaluar el impacto de una amplia gama de intervenciones o introducciones. Por ejemplo, cambios en los procedimientos hospitalarios o la introducción de una nueva cepa de enfermedad en una población.
En este ejemplo, supondremos que se introdujo una nueva cepa de Campylobacter en Alemania a finales de 2008, y veremos si eso afecta al número de casos. Volveremos a utilizar la regresión binomial negativa. Esta vez, la regresión se dividirá en dos partes, una antes de la intervención (o introducción de la nueva cepa en este caso) y otra después (los períodos anterior y posterior). Esto nos permite calcular una tasa de incidencia comparando los dos periodos de tiempo. Explicar la ecuación podría aclararlo (si no es así, ignórala).
La regresión binomial negativa puede definirse como sigue:
\[\log(Y_t)= β_0 + β_1 \times t+ β_2 \times δ(t-t_0) + β_3\times(t-t_0 )^+ + log(pop_t) + e_t\]
Donde: \((Y_t\)) es el número de casos observados en el momento \((t\)) \((pop_t\)) es el tamaño de la población en 100.000s en el momento \((t\)) (no se utiliza aquí) \((t_0\)) es el último año del preperíodo (incluyendo el tiempo de transición si lo hay) \((δ(x\)) es la función indicadora (es 0 si x≤0 y 1 si x\(>0)\)((x)\(^+\)) es el operador de corte (es x si x\(>0 y 0 en caso contrario)\)(e_t$) denota el residuo
Se pueden añadir los términos adicionales tendencia y estación según sea necesario.
\(β_2 \times δ(t-t_0) + β_3\times(t-t_0 )^+\) es la parte lineal generalizada del periodo posterior y es cero en el periodo anterior. Esto significa que las estimaciones \(β_2\) y \(β_3\) son los efectos de la intervención.
Aquí tenemos que volver a calcular los términos de Fourier sin previsión, ya que utilizaremos todos los datos de que disponemos (es decir, a posteriori). Además, tenemos que calcular los términos adicionales necesarios para la regresión.
## añade los términos de fourier utilizando las variables epiweek y case_int
counts$fourier <- select(counts, epiweek, case_int) %>%
as_tsibble(index = epiweek) %>%
fourier(K = 1)
## define la semana de intervención
intervention_week <- yearweek("2008-12-31")
## define variables para la regresión
counts <- counts %>%
mutate(
## corresponde a t en la fórmula
## recuento de semanas (probablemente también se podría usar directamente la variable epiweek)
# linear = row_number(epiweek),
## corresponde a delta(t-t0) en la fórmula
## periodo anterior o posterior a la intervención
intervention = as.numeric(epiweek >= intervention_week),
## corresponde a (t-t0)^+ en la fórmula
## recuento de semanas posteriores a la intervención
## ( elige el número mayor entre 0 y lo que resulte del cálculo)
time_post = pmax(0, epiweek - intervention_week + 1))A continuación, utilizamos estos términos para ajustar una regresión binomial negativa y elaboramos una tabla con el porcentaje de cambio. Lo que muestra este ejemplo es que no hubo ningún cambio significativo.
ATENCIÓN: Observa el uso de simulate_pi = FALSE dentro del argumento de predict(). Esto se debe a que el comportamiento por defecto de la tendencia es utilizar el paquete ciTools para estimar un intervalo de predicción. Esto no funciona si hay recuentos NA, y también produce intervalos más granulares. Véase ?trending::predict.trending_model_fit para más detalles.
## define el modelo que se quiere ajustar (binomial negativo)
model <- glm_nb_model(
## establece el número de casos como resultado de interés
case_int ~
## utiliza epiweek para tener en cuenta la tendencia
epiweek +
## utiliza los términos furier para tener en cuenta la estacionalidad
fourier +
## añade si está en el periodo anterior o posterior
intervention +
## añade el tiempo posterior a la intervención
time_post
)
## ajusta el modelo utilizando el conjunto de datos de recuentos
fitted_model <- trending::fit(model, counts)
## calcula los intervalos de confianza y de predicción
observed <- predict(fitted_model, simulate_pi = FALSE)## muestra las estimaciones y el porcentaje de cambio en una tabla
fitted_model %>%
## extrae la regresión binomial negativa original
get_model() %>%
## obtiene un dataframe ordenado de los resultados
tidy(exponentiate = TRUE,
conf.int = TRUE) %>%
## conserva sólo el valor de intervención
filter(term == "intervention") %>%
## cambia la TIR (IRR) por el porcentaje de cambio para la estimación y los IC
mutate(
## para cada una de las columnas de interés - crea una nueva columna
across(
all_of(c("estimate", "conf.low", "conf.high")),
## aplica la fórmula para calcular el cambio porcentual
.f = function(i) 100 * (i - 1),
## añade un sufijo a los nuevos nombres de columna con "_perc"
.names = "{.col}_perc")
) %>%
## sólo mantiene (y renombra) ciertas columnas
select("IRR" = estimate,
"95%CI low" = conf.low,
"95%CI high" = conf.high,
"Percentage change" = estimate_perc,
"95%CI low (perc)" = conf.low_perc,
"95%CI high (perc)" = conf.high_perc,
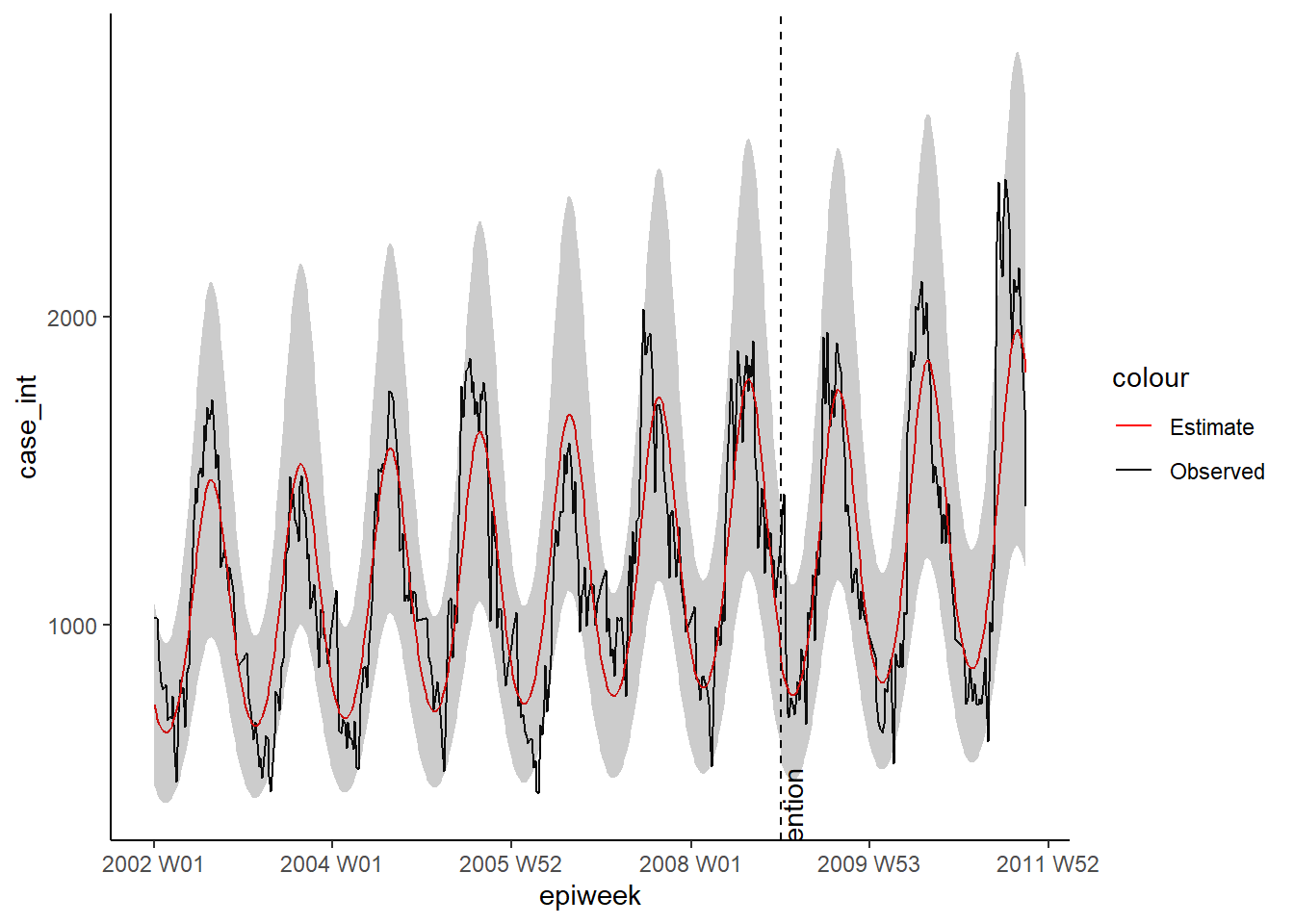
"p-value" = p.value)Como en el caso anterior, podemos visualizar los resultados de la regresión.
estimate_res <- data.frame(observed$result)
ggplot(estimate_res, aes(x = epiweek)) +
## añade los recuentos de casos observados como una línea
geom_line(aes(y = case_int, colour = "Observed")) +
## añade una línea para la estimación del modelo
geom_line(aes(y = estimate, col = "Estimate")) +
## añade una banda para los intervalos de predicción
geom_ribbon(aes(ymin = lower_pi,
ymax = upper_pi),
alpha = 0.25) +
## añade una línea vertical y una etiqueta para mostrar dónde empezó la predicción
geom_vline(
xintercept = as.Date(intervention_week),
linetype = "dashed") +
annotate(geom = "text",
label = "Intervention",
x = intervention_week,
y = max(observed$upper_pi),
angle = 90,
vjust = 1
) +
## define los colores
scale_colour_manual(values = c("Observed" = "black",
"Estimate" = "red")) +
## realiza un gráfico tradicional (con ejes negros y fondo blanco)
theme_classic()Warning: Unknown or uninitialised column: `upper_pi`.Warning in max(observed$upper_pi): no non-missing arguments to max; returning
-Inf23.9 Recursos
Forecasting: principles and practice. Libro de texto